
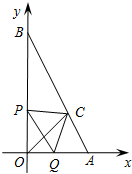
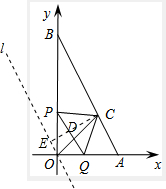
 如图,已知点A(2,0)、B(0,4),一点P距离O点2t个单位(0<t<2),过点P作平行于AB的直线交x轴于点Q.
如图,已知点A(2,0)、B(0,4),一点P距离O点2t个单位(0<t<2),过点P作平行于AB的直线交x轴于点Q.| 5 |
| 9 |
| OP |
| OB |
| OQ |
| OA |
| 4 |
| 3 |
| 4 |
| 3 |
| 4 |
| 3 |
| OP•OQ |
| PQ |
2
| ||
| 5 |
| DE |
| DC |
| OQ |
| QA |
2
| ||
| 5 |
| 5 |
| 9 |
| 1 |
| 2 |
| 5 |
| 5 |
| 9 |
| 1 |
| 3 |
| 5 |
| 3 |
| 1 |
| 3 |


 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,已知直线y=(1-k)x+k(k<1)与双曲线y=
如图,已知直线y=(1-k)x+k(k<1)与双曲线y=| 6 |
| x |
查看答案和解析>>
科目:初中数学 来源: 题型:
| 与标准质量的差值 (单位:千克) | -3 | -2 | -1.5 | 0 | 1 | 2.5 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 如图所示,菱形ABCD的对角线相交于点O,E、F在线段BD上,且BE=DF,判断四边形AECF是不是中心对称图形?如果不是,请说明理由;如果是,求出对称中心.
如图所示,菱形ABCD的对角线相交于点O,E、F在线段BD上,且BE=DF,判断四边形AECF是不是中心对称图形?如果不是,请说明理由;如果是,求出对称中心.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com