
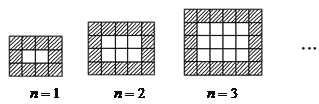
【题目】如图,用同样规格的黑白两色正方形瓷砖铺设长方形地面.请观察各图形并解答有关问题:
(1)在第![]() 个图形中,每一横行共有 块瓷砖,每一竖列共有 块瓷砖(均用含
个图形中,每一横行共有 块瓷砖,每一竖列共有 块瓷砖(均用含![]() 的代数式表示);
的代数式表示);
(2)设铺设地面所用瓷砖的总块数为![]() ,用(1)中的
,用(1)中的![]() 表示
表示![]() ;
;
(3)当![]() =20时,求
=20时,求![]() 的值;
的值;
(4)若黑瓷砖每块4元,白瓷砖每块3元,在问题(3)中,共需花多少元购买瓷砖?
【答案】(1)![]() ,
,![]() ;(2)
;(2)![]() ;(3)506;(4)共需花1604元购买瓷砖.
;(3)506;(4)共需花1604元购买瓷砖.
【解析】
(1)观察图形可得:n=1时,横行有(1+3)块,数列有(1+2)块,以此类推可得出规律;
(2)用每行的块数乘以每列的块数即可得到总块数;
(3)将![]() =20代入(2)中代数式求解即可;
=20代入(2)中代数式求解即可;
(4)由图形规律找到第n个图形中白瓷砖块数,总数减去白瓷砖块数等于黑瓷砖块数,再根据单价求费用即可.
解:(1)观察图形可得:n=1时,横行有(1+3)块,竖列有(1+2)块,
n=2时,横行有(2+3)块,竖列有(2+2)块,
n=3时,横行有(3+3)块,竖列有(3+2)块,
……
以此类推,第n个图中,每一横行有![]() 块,竖列有
块,竖列有![]() 块,
块,
故答案为:![]() ,
,![]() .
.
(2)![]()
(3)当![]() 时,
时,![]()
(4)由图可知:
每一横行有白瓷砖![]() 块,每一竖列有白瓷砖n块,所以白瓷砖总数是
块,每一竖列有白瓷砖n块,所以白瓷砖总数是![]() 块,
块,
当![]() =20时,黑白瓷砖共有506块,白瓷砖有
=20时,黑白瓷砖共有506块,白瓷砖有![]() 块,所以黑瓷砖有506-420=86块,
块,所以黑瓷砖有506-420=86块,
所以共需花86×4+420×3=1604元购买瓷砖.


 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案 金版课堂课时训练系列答案
金版课堂课时训练系列答案 单元全能练考卷系列答案
单元全能练考卷系列答案 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案科目:初中数学 来源: 题型:
【题目】字母m、n分别表示一个有理数,且m≠n.现规定min{m,n}表示m、n中较小的数,例如:min{3,﹣1}=﹣1,min{﹣1,0}=﹣1.据此解决下列问题:
(1)min{﹣![]() ,﹣
,﹣![]() }= .
}= .
(2)若min{![]() ,2)=﹣1,求x的值;
,2)=﹣1,求x的值;
(3)若min{2x﹣5,x+3}=﹣2,求x的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】乔亚萍和张红武做游戏,乔亚萍说:“你在心中想好一个两位数,对这个两位数进行如下的运算:①这个两位数的十位数字和个位数字相加,将所得的和乘以11;②用原两位数的十位数字减去个位数字,将所得的差乘以9;③用①中所得的结果减去②中所得的结果,所得的差加上16,得到最终的结果,把这个结果告诉我,我就能猜出你心中想的数了.”张红武算的结果为50,请帮乔亚萍算出张红武心中想的数为________.
查看答案和解析>>
科目:初中数学 来源: 题型:
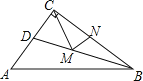
【题目】如图,△ABC中,∠ACB=90°,AC =3,BC =4,AB=5,BD平分∠ABC,如果M、N分别为BD、BC上的动点,那么CM+MN的最小值是____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知在纸面上有一数轴(如图),折叠纸面.
(1)若1表示的点与﹣1表示的点重合,则﹣2.5表示的点与数 表示的点重合;
(2)若﹣1表示的点与5表示的点重合,回答以下问题:
①5表示的点与数 表示的点重合;
②若数轴上A、B两点之间的距离为9(A在B的左侧),且A、B两点经折叠后重合,求A、B两点表示的数是多少?
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了节约用水,某市决定调整居民用水收费方法,规定如果每户每月用水不超过10吨,每吨水收费2元,如果每户每月用水超过10吨,则超过部分每吨水收费2.5元;小红看到这种收费方法后,想算算她家每月的水费:
(1)如果小红家每月用水8吨,则水费是 元;如果小红家每月用水20吨,则水费是 元.
(2)如果字母![]() 表示小红家每月用水的吨数,那么小红家每月的水费该如何用
表示小红家每月用水的吨数,那么小红家每月的水费该如何用![]() 的代数式表示呢?
的代数式表示呢?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】列方程(组)解应用题:
为顺利通过国家义务教育均衡发展验收,我市某中学配备了两个多媒体教室,购买了笔记本电脑和台式电脑共120台,购买笔记本电脑用了7.2万元,购买台式电脑用了24万元,已知笔记本电脑单价是台式电脑单价的1.5倍,那么笔记本电脑和台式电脑的单价各是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】请认真阅读下列材料,再解决后面的问题.
依照平方根(即二次方根)和立方根(即三次方根)的定义,可给出四次方根、五次方根的定义.比如:若x2=a(a≥0),则x叫a的二次方根;若x3=a,则x叫a的三次方根:若x4=a(a≥0),则x叫a的四次方根;
(1)依照上面的材料,请你给出五次方根的定义,并求出﹣32的五次方根;
(2)解方程:![]() (2x﹣4)4﹣8=0
(2x﹣4)4﹣8=0
查看答案和解析>>
科目:初中数学 来源: 题型:
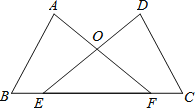
【题目】(1)如图,点E.F在BC上,BE=CF,AB=DC,∠B=∠C.求证:∠A=∠D.
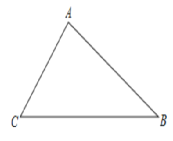
(2)已知如图,在△ABC中,∠B=30°,∠C=45°,ABAC=2![]() ,求BC的长.
,求BC的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com