
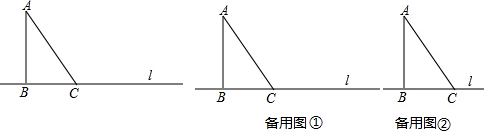
分析 首先根据勾股定理求出AC,然后利用分类讨论的思想来解决,即当CP=CA,AP=AC,PA=PC时分别求出即可.
解答 解:∵∠ABC=90°,BC=3cm,AB=4cm,
∴AC=5cm,
当CP=CA时,2t=8或2t=2,
解得:t=4或1,
当AP=AC时,2t=3,
解得:t=$\frac{3}{2}$,
当PA=PC时,(2t+3)2=(2t)2+42,
解得:t=$\frac{7}{12}$.
综上所述,当t=4或1或$\frac{3}{2}$或$\frac{7}{12}$时,△ACP是等腰三角形.
点评 此题主要考查了勾股定理的应用以及等腰三角形的性质和一元二次方程的应用等知识,利用分类讨论得出是解题关键.


 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
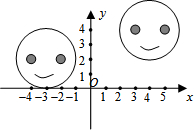 如图,在直角坐标系中,右边的图案是由左边的图案经过平移得到的,左图案中左、右眼睛的坐标分别是(-4,2),(-2,2),右图案中的左眼的坐标是(3,4),则右图案中右眼的坐标是( )
如图,在直角坐标系中,右边的图案是由左边的图案经过平移得到的,左图案中左、右眼睛的坐标分别是(-4,2),(-2,2),右图案中的左眼的坐标是(3,4),则右图案中右眼的坐标是( )| A. | (5,3) | B. | (4,5) | C. | (5,4) | D. | (6,4) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com