
���� ��1�����������ߵĶԳ��������D�ĺ����꣬�ٴ���ֱ��y=-$\frac{1}{2}$x-1���ٽ�A��D����������ʽy=ax2+bx��a��0�����ݴ˼�����������ߵĽ���ʽ��
��2���Ȼ���ͼ���������B�ĶԳƵ�B������꣬��������֮��С�ڵ����ߣ��Լ������ߵĶԳ��Կ�֪����C��ֱ��AB���ϣ��ݴ˽��н�ɵý⣻
��3�����������ߵĶԳ��ԣ��Լ��������ε�֪ʶ���н�𣬾ݴ˼��ɵý⣮
��� �⣺��1����ͼ1����A��4��0����
��OA=4
�������߶Գ��Կ�֪ OH=HA=2
��D�������Ϊ2��
�ߵ�D��ֱ��$y=-\frac{1}{2}x-1$��
��$y=-\frac{1}{2}��2-1=-2$��
��D��2��-2����
��y=ax2+bx����A��4��0����D��2��-2����
��$\left\{\begin{array}{l}{16a+4b=0}\\{4a-2b=-2}\end{array}\right.$��
��$\left\{\begin{array}{l}{a=\frac{1}{2}}\\{b=-2}\end{array}\right.$
��$y=\frac{1}{2}{x}^{2}-2x$��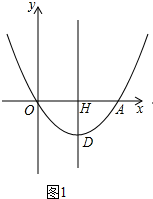
��2����ͼ2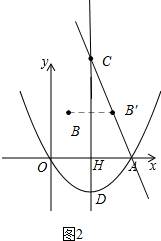
��B���������ߵĶԳ���ĶԳƵ�B��������ǣ�3��3����
��ֱ��AB��Ľ���ʽΪ��y=kx+b��
����A��4��0���͵�B�䣨3��3������ɵã�
$\left\{\begin{array}{l}{4k+b=0}\\{3k+b=3}\end{array}\right.$��
��ã�$\left\{\begin{array}{l}{k=-3}\\{b=12}\end{array}\right.$��
��ֱ��AB��Ľ���ʽΪ��y=-3x+12��
��Գ���Ľ��������ǣ�C��2��6����
��ʱ|AC-BC|��ֵ���
��C��2��6����
��3����ͼ3��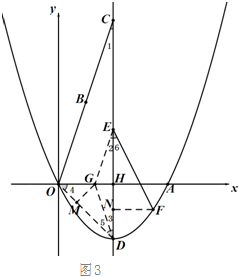
�ߡ�FEC-��BCD=135�㣬
��180��-��DEF-��BCD=135�㣬
���DEF+��BCD=45�㣬
��C��2��6����
��OH=2��CH=6��
��tan��1=$\frac{1}{3}$��
��EG��CO��x����G������GD
�ɶԳ��Կ�֪GE=GD��HE=HD=2��
���2=��3
��tan��2=$\frac{GH}{EH}=\frac{1}{3}$��
��GH=$\frac{2}{3}$��OG=$\frac{4}{3}$��
��OH=HD��
���4=��ODH=45�㣬OD=$\sqrt{{2}^{2}+{2}^{2}}=2\sqrt{2}$
��GM��OD��M����Rt��GOM��
sin��4=$\frac{GM}{OG}=\frac{\sqrt{2}}{2}$��
��GM=$\frac{2\sqrt{2}}{3}$��
��OM=$\sqrt{��\frac{4}{3}��^{2}-��\frac{2\sqrt{2}}{3}��^{2}}=\frac{2\sqrt{2}}{3}$
��MD=$\frac{4\sqrt{2}}{3}$��
��tan��5=$\frac{\frac{2\sqrt{2}}{3}}{\frac{4\sqrt{2}}{3}}=\frac{1}{2}$��
�ߡ�5+��3=45�㣬
���5+��1=45�㣬
���6=��5��
��tan��6=$\frac{1}{2}$��
��FN��ED��N�����F�ĺ�����Ϊt��
��F��t��$\frac{1}{2}{t}^{2}-2t$����
��FN=2-t EN=$-\frac{1}{2}{t}^{2}+2t+2$��$\frac{t-2}{-\frac{1}{2}{t}^{2}+2t+2}=\frac{1}{2}$
��t=��$2\sqrt{3}$��
�ߵ�F�ڶԳ����Ҳ��������ϣ�
��t��2��
��t=$2\sqrt{3}$��
��F�ĺ�����Ϊ$2\sqrt{3}$��
���� ��1������Ҫ�������ô���ϵ�����������ߵĽ���ʽ�����������ߵĶԳ��������D�������ǽ���Ĺؼ�����2���⿼���������������ϵĵ�ĶԳ�������ֵ�����⣬�Լ������ε����߹�ϵ����3������Ҫ�����˽�ֱ�������ε�֪ʶ���Լ��������ϵĵ�ı�ʾ�������ۺ��Ժ�ǿ��Ҫע�������ܽᣮ


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
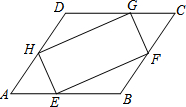 ��ͼ��ƽ���ı���ABCD�У���E��F��G��H�ֱ���AB��BC��CD��DA������AE=AH=CF=CG��AB=AD����֤���ı���EFGH�Ǿ��Σ�
��ͼ��ƽ���ı���ABCD�У���E��F��G��H�ֱ���AB��BC��CD��DA������AE=AH=CF=CG��AB=AD����֤���ı���EFGH�Ǿ��Σ��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
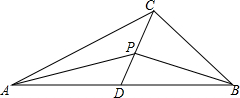 ��ͼ����һ�������ε����߷ֱ���3��1-3m��8��
��ͼ����һ�������ε����߷ֱ���3��1-3m��8���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
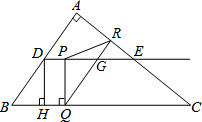 ��ͼ����Rt��ABC�У���A=90�㣬AB=6cm��AC=8cm��D��E�ֱ��DZ�AB��AC���е㣬��P�ӵ�D������DE������1cm/s���ٶ��˶�������P��PQ��BC��Q������Q��QR��BA��AC��R����DE��G������Q���C�غ�ʱ����Pֹͣ�˶������P�˶�ʱ��Ϊts��
��ͼ����Rt��ABC�У���A=90�㣬AB=6cm��AC=8cm��D��E�ֱ��DZ�AB��AC���е㣬��P�ӵ�D������DE������1cm/s���ٶ��˶�������P��PQ��BC��Q������Q��QR��BA��AC��R����DE��G������Q���C�غ�ʱ����Pֹͣ�˶������P�˶�ʱ��Ϊts���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ƽ��ֱ������ϵxOy�У�������y=-$\frac{1}{2}$��x+m��2�Ķ���ΪA��ֱ��y=-x-m��y���ཻ�ڵ�B������m��0��
��ƽ��ֱ������ϵxOy�У�������y=-$\frac{1}{2}$��x+m��2�Ķ���ΪA��ֱ��y=-x-m��y���ཻ�ڵ�B������m��0���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
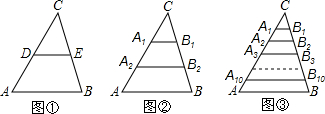
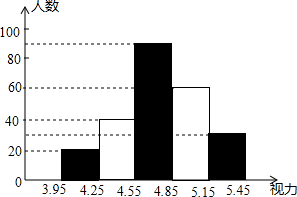 ������������״���ܵ�ȫ���Ĺ㷺��ע��ij���йز��Ŷ�ȫ��24000������������״��������һ�γ������飬��ͼ�������������ݻ��Ƶ�Ƶ���ֲ�ֱ��ͼ�������εĸ߱�ʾ����������������ͼ�����ṩ����Ϣ���ش��������⣺
������������״���ܵ�ȫ���Ĺ㷺��ע��ij���йز��Ŷ�ȫ��24000������������״��������һ�γ������飬��ͼ�������������ݻ��Ƶ�Ƶ���ֲ�ֱ��ͼ�������εĸ߱�ʾ����������������ͼ�����ṩ����Ϣ���ش��������⣺�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com