
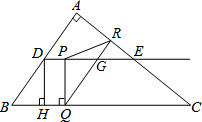
 如图,在Rt△ABC中,∠A=90°,AB=6cm,AC=8cm,D,E分别是边AB,AC的中点,点P从点D出发沿DE方向以1cm/s的速度运动,过点P作PQ⊥BC于Q,过点Q作QR∥BA交AC于R,交DE于G,当点Q与点C重合时,点P停止运动.设点P运动时间为ts.
如图,在Rt△ABC中,∠A=90°,AB=6cm,AC=8cm,D,E分别是边AB,AC的中点,点P从点D出发沿DE方向以1cm/s的速度运动,过点P作PQ⊥BC于Q,过点Q作QR∥BA交AC于R,交DE于G,当点Q与点C重合时,点P停止运动.设点P运动时间为ts.分析 (1)根据三角形相似的判定定理求出△BHD∽△BAC,根据相似三角形的性质求出DH的长;
(2)根据D,E分别是边AB,AC的中点,得到DE∥BC,得到四边形BQGD是平行四边形,于是得到当BD=BQ时.?BQGD是菱形,即可得到t的值,如图1,过P作PN⊥QR于N,由△PQN∽△ABC,求得PN=$\frac{36}{25}$,由△CQR∽△CBA,求得RQ=$\frac{21}{5}$,即可得到结果;
(3)根据△RQC∽△ABC,根据三角形的相似比求出y关于t的函数关系式;
(4)画出图形,根据图形进行讨论:①当PQ=PR时,过点P作PM⊥QR于M,则QM=RM.由于∠1+∠2=90°,∠C+∠2=90°,得到∠1=∠C.于是得到cos∠1=cosC=$\frac{8}{10}$=$\frac{4}{5}$,根据$\frac{QM}{QP}$=$\frac{4}{5}$,即可求出t的值;②当PQ=RQ时,-$\frac{3}{5}$t+$\frac{123}{25}$=$\frac{12}{5}$,即可求出t的值;③当PR=QR时,则R为PQ中垂线上的点,于是点R为EC的中点,故CR=$\frac{1}{2}$CE=$\frac{1}{4}$AC=2.由于tanC=$\frac{QR}{CR}$=$\frac{BA}{CA}$,即可得到结果.
解答 解:(1)在Rt△ABC中,
∵∠A=90°,AB=6,AC=8,
∴BC=$\sqrt{A{B}^{2}+A{C}^{2}}$=10.
∵∠DHB=∠A=90°,∠B=∠B.
∴△BHD∽△BAC,
∴$\frac{DH}{AC}$=$\frac{BD}{BC}$,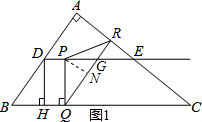
∴DH=$\frac{BD}{BC}$•AC=$\frac{3}{10}$×8=$\frac{12}{5}$;
故答案为:$\frac{12}{5}$;
(2)∵D,E分别是边AB,AC的中点,
∴DE∥BC,
∵QR∥AB,
∴四边形BQGD是平行四边形,
∴当BD=BQ时.?BQGD是菱形,
∵AB=6cm,AC=8cm,
∴tanB=$\frac{AC}{AB}$=$\frac{4}{3}$,
∴$\frac{DH}{BH}$=$\frac{4}{3}$,
∵BD=$\frac{1}{2}$AB=3,BH=$\frac{3}{5}$BD=$\frac{9}{5}$,
∴3=t+$\frac{9}{5}$,
∴t=$\frac{6}{5}$,
∴当四边形BQGD是菱形时,t=$\frac{6}{5}$,
如图1,过P作PN⊥QR于N,
∴∠PQN+∠RQC=∠RQC+∠C=90°,
∴∠PQN=∠C,
∴△PQN∽△ABC,
∴$\frac{PQ}{BC}=\frac{PN}{AB}$,
∵PQ=DH=$\frac{12}{5}$,
∴$\frac{\frac{12}{5}}{10}=\frac{PN}{6}$,
∴PN=$\frac{36}{25}$,
∵RQ∥AB,
∴△CQR∽△CBA,
∴$\frac{CQ}{CB}=\frac{RQ}{AB}$,
∵CQ=BC-BQ=7,
∴$\frac{7}{10}=\frac{RQ}{6}$,
∴RQ=$\frac{21}{5}$,
∴S△PQR=$\frac{1}{2}$QR•PN=$\frac{1}{2}×\frac{36}{25}×\frac{21}{5}$=$\frac{378}{125}$,
故答案为:$\frac{3}{2}$,$\frac{378}{125}$,
(3)∵QR∥AB,
∴∠QRC=∠A=90°.
∵∠C=∠C,
∴△RQC∽△ABC,
∴$\frac{RQ}{AB}$=$\frac{QC}{BC}$,
∵BH=$\sqrt{B{D}^{2}-D{H}^{2}}$=$\frac{9}{5}$,
∴BQ=$\frac{9}{5}$+t,
∴$\frac{y}{6}$=$\frac{10-\frac{9}{5}-t}{10}$,
即y关于x的函数关系式为:y=-$\frac{3}{5}$t+$\frac{123}{25}$;
(4)存在,分三种情况:
①如图2当PQ=PR时,过点P作PM⊥QR于M,则QM=RM.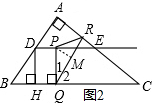
∵∠1+∠2=90°,∠C+∠2=90°,
∴∠1=∠C.
∴cos∠1=cosC=$\frac{8}{10}$=$\frac{4}{5}$,
∴$\frac{QM}{QP}$=$\frac{4}{5}$,
∴$\frac{\frac{1}{2}(-\frac{3}{5}t+\frac{123}{25})}{\frac{12}{5}}$=$\frac{4}{5}$,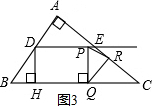 ∴t=$\frac{9}{5}$.
∴t=$\frac{9}{5}$.
②如图3,当PQ=RQ时,-$\frac{3}{5}$t+$\frac{123}{25}$=$\frac{12}{5}$,
∴t=$\frac{21}{5}$.
③如图4,作EM⊥BC,RN⊥EM,
∴EM∥PQ,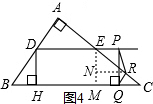 当PR=QR时,则R为PQ中垂线上的点,
当PR=QR时,则R为PQ中垂线上的点,
∴EN=MN,
∴ER=RC,
∴点R为EC的中点,
∴CR=$\frac{1}{2}$CE=$\frac{1}{4}$AC=2.
∵tanC=$\frac{QR}{CR}$=$\frac{BA}{CA}$,
∴$\frac{-\frac{3}{5}t+\frac{123}{25}}{2}$=$\frac{6}{8}$,
∴t=$\frac{73}{3}$.
综上所述,当t为$\frac{9}{5}$或$\frac{21}{5}$或$\frac{73}{3}$时,△PQR为等腰三角形.
点评 本题考查了相似三角形的判定和性质,锐角三角函数,等腰三角形的性质,解答此题的关键是根据题意画出图形,用数形结合的方法解答.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 目标测试系列答案
目标测试系列答案科目:初中数学 来源: 题型:解答题
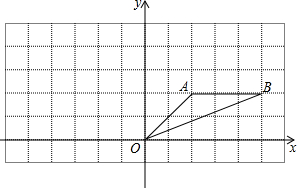 如图在平面直角坐标系中,已知点A(2,2),B(5,2).
如图在平面直角坐标系中,已知点A(2,2),B(5,2).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
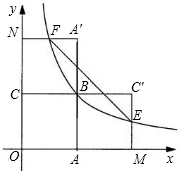 如图,四边形OABC是面积为4的正方形,双曲线经过点B.
如图,四边形OABC是面积为4的正方形,双曲线经过点B.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
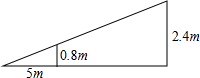 如图,小芳在达网球时,为使球恰好能过网(网高0.8米),且落在对方区域内离网5米的位置上,如果她的击球高度是2.4米,则应站在离网的( )
如图,小芳在达网球时,为使球恰好能过网(网高0.8米),且落在对方区域内离网5米的位置上,如果她的击球高度是2.4米,则应站在离网的( )| A. | 15米处 | B. | 10米处 | C. | 8米处 | D. | 7.5米处 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com