
分析 由已知条件易求∠BAD=120°,菱形的每条对角线平分一组对角,则∠BAO=$\frac{1}{2}$∠BAD=60°,即△ABC是等边三角形,由此可求得AC=AB=2cm;由菱形的性质可知:菱形的对角线互相垂直平分,在Rt△BAO中,已知AB、AO的长,由勾股定理求得BO的长,进而可得出菱形ABCD的面积.
解答 解:∵四边形ABCD是菱形,∠ABC=60°,
∴∠BAD=120°,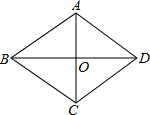
∴∠BAO=$\frac{1}{2}$∠BAD=$\frac{1}{2}$×120°=60°,
又在△ABC中,AB=BC,
∴∠BCA=∠BAC=60°,
∠ABC=180°-∠BCA-∠BAC=60°,
∴△ABC为等边三角形,
∴AC=AB=2cm,
在菱形ABCD中,AC⊥BD,
∴△AOB为直角三角形,
∴OB2=AB2-AO2,
∴OB=$\sqrt{3}$cm,
∴BD=2BO=2$\sqrt{3}$cm,
∴S菱形ABCD=$\frac{1}{2}$AC•BD=$\frac{1}{2}$×2×2$\sqrt{3}$=2$\sqrt{3}$cm2.
点评 本题主要考查的是菱形的性质:菱形的四条边都相等;对角线互相垂直平分;每条对角线平分一组对角.熟记菱形的面积等于对角线乘积的一半是解题的关键.


 教材全解字词句篇系列答案
教材全解字词句篇系列答案科目:初中数学 来源: 题型:解答题
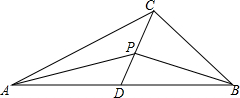 如图,设一个三角形的三边分别是3,1-3m,8.
如图,设一个三角形的三边分别是3,1-3m,8.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
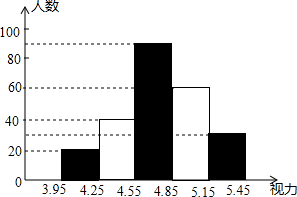 初中生的视力状况受到全社会的广泛关注,某市有关部门对全市24000名初中生视力状况进行了一次抽样调查,如图是利用所得数据绘制的频数分布直方图(长方形的高表示该组人数),根据图中所提供的信息,回答下列问题:
初中生的视力状况受到全社会的广泛关注,某市有关部门对全市24000名初中生视力状况进行了一次抽样调查,如图是利用所得数据绘制的频数分布直方图(长方形的高表示该组人数),根据图中所提供的信息,回答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
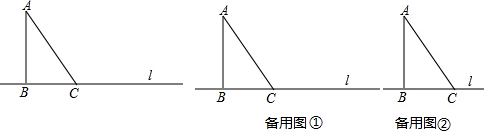
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
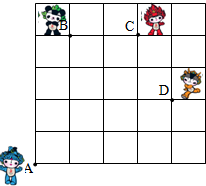 如图,奥运福娃在5×5的方格(每小格边长为1m)上沿着网格线运动.贝贝从A处出发去寻找B、C、D处的其它福娃,规定:向上向右走为正,向下向左走为负.如果从A到B记为:A→B(+1,+4),从B到A记为:B→A(-1,-4),其中第一个数表示左右方向,第二个数表示上下方向,那么图中
如图,奥运福娃在5×5的方格(每小格边长为1m)上沿着网格线运动.贝贝从A处出发去寻找B、C、D处的其它福娃,规定:向上向右走为正,向下向左走为负.如果从A到B记为:A→B(+1,+4),从B到A记为:B→A(-1,-4),其中第一个数表示左右方向,第二个数表示上下方向,那么图中查看答案和解析>>
科目:初中数学 来源: 题型:填空题
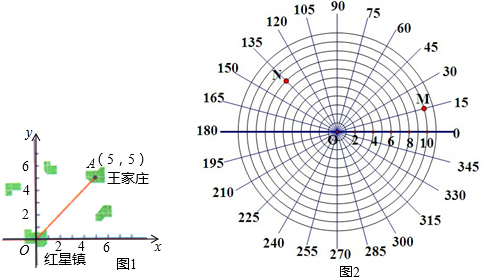
 如图是一组密码的一部分,为了保密,许多情况下可采用不同的密码,请你运用所学数学知识找到破译密码的“钥匙”,目前,已破译处“正做数学”的真实意义是“”祝你成功,若“正”所处的位置为(x,y),你找到的密码钥匙是(x-1,y-2),破译的“今天考试”真实意思是努力发挥.
如图是一组密码的一部分,为了保密,许多情况下可采用不同的密码,请你运用所学数学知识找到破译密码的“钥匙”,目前,已破译处“正做数学”的真实意义是“”祝你成功,若“正”所处的位置为(x,y),你找到的密码钥匙是(x-1,y-2),破译的“今天考试”真实意思是努力发挥.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com