练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图所示，在△ABC中，∠CAB=70°，现将△ABC绕点A顺时针旋转一定角度后得到△AB′C′，连接BB′，若BB′∥AC′，则∠CAB′的度数为（ ）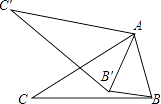
    A.20°
    B.25°
    C.30°
    D.40°

    【答案】C
    【解析】解：由旋转的性质得：∠C′AB′=∠CAB=70°，AB′=AB， ∴∠AB′B=∠ABB′，
    ∵BB′∥AC′，
    ∴∠AB′B=∠C′AB′=70°，
    ∴∠ABB′=70°，
    ∴∠BAB′=180°﹣70°﹣70°=40°，
    ∴∠CAB′=∠CAB﹣∠BAB′=70°﹣40°=30°；
    故选：C．
    由旋转的性质得出∠C′AB′=∠CAB=70°，AB′=AB，得出∠AB′B=∠ABB′，由平行线得出∠AB′B=∠C′AB′=70°，由三角形内角和求出∠BAB′，即可得出∠CAB′的度数．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图，D为△ABC内一点，CD平分∠ACB，BD⊥CD，∠A=∠ABD，若AC=5，BC=3，则BD的长为（　　）

    A. 1 B. C. D. 4

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，二次函数y=ax2+bx+c的图象开口向上，对称轴为直线x=1，图象经过（3，0），下列结论中，正确的一项是（ ）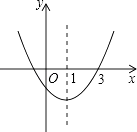
    A.abc＜0
    B.4ac﹣b2＜0
    C.a﹣b+c＜0
    D.2a+b＜0

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图所示，一个四边形纸片ABCD，∠B=∠D=90°，把纸片按如图所示折叠，使点B落在AD边上的B'点，AE是折痕。

    （1）试判断B'E与DC的位置关系并说明理由。

    （2）如果∠C=130°，求∠AEB的度数。

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】阅读下面材料：

    在数学课上，老师提出如下问题：

    尺规作图：作对角线等于已知线段的菱形．

    已知：两条线段a、b．

    求作：菱形AMBN,使得其对角线分别等于b和2a．

    尺规作图：作对角线等于已知线段的菱形．

    已知：两条线段a、b．

    求作：菱形AMBN,使得其对角线分别等于b和2a．

    小军的作法如下：

    如图

    (1)画一条线段AB等于b；

    (2)分别以A、B为圆心，大于AB的长为半径，

    在线段AB的上下各作两条弧，两弧相交于P、Q两点；

    (3)作直线PQ交AB于O点；

    (4)以O点为圆心，线段a的长为半径作两条弧，交直线PQ于M、N两点，连接AM、AN、BM、BN．所以四边形AMBN就是所求的菱形.

    如图

    (1)画一条线段AB等于b；

    (2)分别以A、B为圆心，大于AB的长为半径，

    在线段AB的上下各作两条弧，两弧相交于P、Q两点；

    (3)作直线PQ交AB于O点；

    (4)以O点为圆心，线段a的长为半径作两条弧，交直线PQ于M、N两点，连接AM、AN、BM、BN．所以四边形AMBN就是所求的菱形.

    老师说：“小军的作法正确．”

    该上面尺规作图作出菱形AMBN的依据是_______________________________

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知：如图，在矩形ABCD中，AB=8，BC=4．在AD上取一点E，AE=1，点F是AB边上的一个动点，以EF为一边作菱形EFMN，使点N落在CD边上，点M落在矩形ABCD内或其边上．若AF=x，△BFM的面积为S．

    （1）当四边形EFMN是正方形时，求x的值；

    （2）当四边形EFMN是菱形时，求S与x的函数关系式；

    （3）当x= 时，△BFM的面积S最大；当x= 时，△BFM的面积S最小；

    （4）在△BFM的面积S由最大变为最小的过程中，请直接写出点M运动的路线长： 。

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】下面是“求作∠AOB的角平分线”的尺规作图过程．

    已知：如图，钝角∠AOB．

    求作：∠AOB的角平分线．

    作法：

    ①在OA和OB上，分别截取OD、OE，使OD=OE；

    ②分别以D、E为圆心，大于DE的长为半径作弧，在∠AOB内，两弧交于点C；

    ③作射线OC．

    所以射线OC就是所求作的∠AOB的角平分线．

    请回答：该尺规作图的依据是__．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】阅读下列两则材料：

    材料一：我们可以将任意三位数记为（其中a，b，c分别表示该数百位数字、十位数字和个位数字，且a≠0），显然=100a+10b+c．

    材料二：若一个三位数的百位数字、十位数字和个位数字均不为0，则称之为原始数，比如123就是一个原始数，将原始数的三个数位上的数字交换顺序，可产生出5个原始数，比如由123可以产生出132，213，231，312，321这5个原始数．将这6个数相加，得到的和1332称为由原始数123生成的终止数．利用材料解决下列问题：

    （1）分别求出由下列两个原始数生成的终止数：243，537；

    （2）若一个原始数的终止数是另一个原始数的终止数的3倍，分别求出所有满足条件的这两个原始数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某学校小组利用暑假中前40天参加社会实践活动，参与了一家网上书店经营，了解到一种成本每本20元的书在x天销售量P=50﹣x．在第x天的售价每本y元，y与x的关系如图所示． 已知当社会实践活动时间超过一半后．y=20+
    （1）请求出当1≤x≤20时，y与x的函数关系式，并求出第12天此书的销售单价；
    （2）这40天中该网点销售此书第几天获得的利润最大？最大的利润是多少？

    查看答案和解析>>

    同步练习册答案