
【题目】已知:如图,在矩形ABCD中,AB=8,BC=4.在AD上取一点E,AE=1,点F是AB边上的一个动点,以EF为一边作菱形EFMN,使点N落在CD边上,点M落在矩形ABCD内或其边上.若AF=x,△BFM的面积为S.
(1)当四边形EFMN是正方形时,求x的值;

(2)当四边形EFMN是菱形时,求S与x的函数关系式;

(3)当x= 时,△BFM的面积S最大;当x= 时,△BFM的面积S最小;
(4)在△BFM的面积S由最大变为最小的过程中,请直接写出点M运动的路线长: 。


【答案】(1)x=3;(2)S=![]() ;(3)
;(3)![]() ;(4)
;(4) ![]()
【解析】
(1)利用AAS证明△DEN≌△AFE即可解决问题;
(2)如图,过点M作MH⊥AB于H,连接NF,证明△DEN≌△HMF,可得MH=DE=3,由此即可解决问题;
(3)①如备用图①中,当点N与点D重合时,x的值最小,△FBM的面积最大,在Rt△AEF中,x=![]() ,推出S的最大值=12-3
,推出S的最大值=12-3![]() ;②如备用图②,当点M在BC上时,x的值最大,△FBM的面积最小;
;②如备用图②,当点M在BC上时,x的值最大,△FBM的面积最小;
(4)如备用图③中,在△BFM的面积S由最大变为最小的过程中,点M的运动轨迹是平行AB的线段,点M运动的路线长=BF的长=8-2![]() .
.
(1)在正方形EFMN中,∠FEN=90°,EF=EN,
∴ ∠DEN+∠AEF=90°,
在矩形ABCD中,∠A=∠D=90°,
∴ ∠AEF+∠AFE=90°,
∴ ∠DEN=∠AFE,
在△DEN与△AFE中,
 ,
,
∴△DEN≌△AFE(AAS),
∴AF=DE=4-1=3,
∴x的值为3;
(2)过点M作MH⊥AB于H,连接NF,
在矩形ABCD中,∵AB∥CD,
∴∠DNF=∠NFB,
∵四边形EFMN是菱形,
∴NE‖MF ,NE=MF,
∴∠ENF=∠MFN,
∴∠DNE=∠MFB ,
在△DEN与△HMF中,
 ,
,
∴△DEN≌△HMF(AAS),
∴MH=DE=3,BF=8-x,
![]() ;
;

(3)①如备用图①中,当点N与点D重合时,x的值最小,△FBM的面积最大,
在Rt△AEF中,x=![]() ,
,
∴S的最大值=12-3![]() ;
;
②如备用图②,当点M在BC上时,x的值最大,△FBM的面积最小,
此时易得CN=AF=x,
∵EN=EF,
∴12+x2=32+(8-x)2,
∴x=![]() ,
,
∴S的最小值为![]() ,
,
故答案为:2![]() ,
,![]() ;
;
(4)如备用图③中,在△BFM的面积S由最大变为最小的过程中,点M的运动轨迹是平行AB的线段,点M运动的路线长=BF的长=8-2![]() ,
,
故答案为:![]() .
.


科目:初中数学 来源: 题型:
【题目】在一款名为超级玛丽的游戏中,玛丽到达一个高为10米的高台A,利用旗杆顶部的绳索,划过90°到达与高台A水平距离为17米,高为3米的矮台B,

(1)求高台A比矮台B高多少米?
(2)求旗杆的高度OM;
(3)玛丽在荡绳索过程中离地面的最低点的高度MN.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图![]() ,
, ![]() 中,
中, ![]() 于
于![]() ,且
,且![]() .
.
(![]() )试说明
)试说明![]() 是等腰三角形.
是等腰三角形.
(![]() )已知
)已知![]() ,如图
,如图![]() ,动点
,动点![]() 从点
从点![]() 出发以每秒
出发以每秒![]() 的速度沿线段
的速度沿线段![]() 向点
向点![]() 运动,同时动点
运动,同时动点![]() 从点
从点![]() 出发以相同速度沿线段
出发以相同速度沿线段![]() 向点
向点![]() 运动,当其中一点到达终点时整个运动都停止.设点
运动,当其中一点到达终点时整个运动都停止.设点![]() 运动的时间为
运动的时间为![]() (秒).
(秒).
①若![]() 的边与
的边与![]() 平行,求
平行,求![]() 的值.
的值.
②若点![]() 是边
是边![]() 的中点,问在点
的中点,问在点![]() 运动的过程中,
运动的过程中, ![]() 能否成为等腰三角形?若能,求出
能否成为等腰三角形?若能,求出![]() 的值;若不能,请说明理由.
的值;若不能,请说明理由.


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,边长为1的正方形EFGH在边长为4的正方形ABCD所在平面上移动,始终保持EF//AB,CK=1.线段KG的中点为M,DH的中点为N,则线段MN的长为 ( ).

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在△ABC中,∠CAB=70°,现将△ABC绕点A顺时针旋转一定角度后得到△AB′C′,连接BB′,若BB′∥AC′,则∠CAB′的度数为( ) 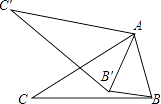
A.20°
B.25°
C.30°
D.40°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某天晚上,小春放学从学校步行回家,走了一段后,小春的同学小佳也从学校骑车回家,随后小佳追上了小春,并邀请小春坐他的自行车一起回家,但遭到了小春的拒绝.随后小佳便下车,推车与小春一起回家.很快小春到家了,小佳与小春道别后也骑上车继续回家.若学校、小春家、小佳家都在同一条笔直的公路上,则从小春出发时算起,小春与小佳的距离y关于时间t的函数图象最可能是下图中的( ).
A.  B.
B.  C.
C.  D.
D. 
查看答案和解析>>
科目:初中数学 来源: 题型:
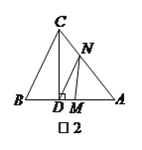
【题目】如图,在△ABC中,AB=BC,AD⊥BC于点D,点E为AC中点且BE平分∠ABD,连接BE交AD于点F,且BF=AC,过点D作DG∥AB,交AC于点G.
求证:
(1)∠BAD=2∠DAC
(2)EF=EG.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】宜宾市某化工厂,现有A种原料52千克,B种原料64千克,现用这些原料生产甲、乙两种产品共20件.已知生产1件甲种产品需要A种原料3千克,B种原料2千克;生产1件乙种产品需要A种原料2千克,B种原料4千克,则生产方案的种数为( )
A.4
B.5
C.6
D.7
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com