
【题目】将一个矩形纸片OABC放置在平面直角坐标系xOy内,点A(6,0),点C(0,4),点O(0,0).点P是线段BC上的动点,将△OCP沿OP翻折得到△OC′P.

(Ⅰ)如图①,当点C′落在线段AP上时,求点P的坐标;
(Ⅱ)如图②,当点P为线段BC中点时,求线段BC′的长度.
【答案】(Ⅰ)P(6﹣2![]() ,4);(Ⅱ)BC′=
,4);(Ⅱ)BC′=![]()
【解析】
(Ⅰ)如图①,证明AO=AP=6,利用勾股定理求出PB即求出点P的坐标.
(Ⅱ)如图②,连接CC′交OP于D.解直角三角形求出PD,利用三角形的中位线定理即可解决问题.
(Ⅰ)∵A(5,0),点C(0,3),
∴OA=6,OC=4,
由翻折可知:∠OPC=∠OPA,
∵BC∥OA,
∴∠OPC=∠OPA,
∴∠POA=∠OPA,
∴OA=PA=6,
在Rt△PAB中,
∵∠B=90°,AB=4,PA=6,
∴PB=![]() =2
=2![]() ,
,
∴PC=BC﹣PB=6﹣2![]() ,
,
∴P(6﹣2![]() ,4).
,4).
(Ⅱ)如图②,连接CC′交OP于D.

在Rt△OPC中,∵OC=4,PC=3,
∴OP=![]() =5,
=5,
∵OP垂直平分线段CC′,
又∵![]() OPCD=
OPCD=![]() OCPC,
OCPC,
∴CD=![]() ,
,
PD=![]() ,
,
∵PC=PB,CD=DC′,
∴BC′=2PD=![]() .
.


 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案科目:初中数学 来源: 题型:
【题目】已知:抛物线![]() :
:![]() (
(![]() 、
、![]() 、
、![]() 为常数,且
为常数,且![]() )与
)与![]() 轴分别交于
轴分别交于![]() ,
,![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() .
.
(1)求抛物线![]() 的表达式;
的表达式;
(2)将![]() 平移后得到抛物线
平移后得到抛物线![]() ,点
,点![]() 、
、![]() 在
在![]() 上(点
上(点![]() 在点
在点![]() 的上方),若以点
的上方),若以点![]() 、
、![]() 、
、![]() 、
、![]() 为顶点的四边形是正方形,求抛物线
为顶点的四边形是正方形,求抛物线![]() 的解析式.
的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有一块锐角三角形卡纸余料ABC,它的边BC=120cm,高AD=80cm,为使卡纸余料得到充分利用,现把它裁剪成一个邻边之比为2:5的矩形纸片EFGH和正方形纸片PMNQ,裁剪时,矩形纸片的较长边在BC上,正方形纸片一边在矩形纸片的较长边EH上,其余顶点均分别在AB,AC上,具体裁剪方式如图所示。
(1)求矩形纸片较长边EH的长;
(2)裁剪正方形纸片时,小聪同学是按以下方法进行裁剪的:先沿着剩余料![]() 中与边EH平行的中位线剪一刀,再沿过该中位线两端点向边EH所作的垂线剪两刀,请你通过计算,判断小聪的剪法是否正确.
中与边EH平行的中位线剪一刀,再沿过该中位线两端点向边EH所作的垂线剪两刀,请你通过计算,判断小聪的剪法是否正确.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校调查了若干名家长对“初中生带手机上学”现象的看法,统计整理并制作了如下的条形与扇形统计图,根据图中提供的信息,完成以下问题:
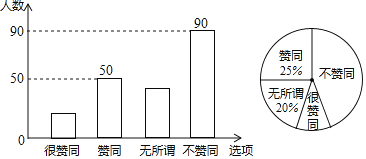
(1)本次共调查了 名家长;扇形统计图中“很赞同”所对应的圆心角是 度.已知该校共有1600名家长,则“不赞同”的家长约有 名;请补全条形统计图;
(2)从“不赞同”的五位家长中(两女三男),随机选取两位家长对全校家长进行“学生使用手机危害性”的专题讲座,请用树状图或列表法求出选中“1男1女”的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】参照学习函数的过程与方法,探究函数![]()
![]() 的图象与性质列表:
的图象与性质列表:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
描点:在平面直角坐标系中,以自变量x的取值为横坐标,以![]() 相应的函数值为纵坐标,描出相应的点,如图所示:
相应的函数值为纵坐标,描出相应的点,如图所示:
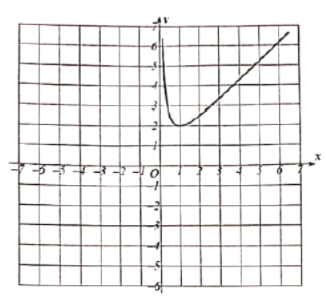
(1)请补全函数图象:
(2)观察图象并分析表格,回答下列问题:
①当![]() 时,y随x的增大而_________;(填“增大”或“减小”)
时,y随x的增大而_________;(填“增大”或“减小”)
②图象关于点__________中心对称.(填点的坐标)
③当![]() 时,
时,![]() 的最小值是_________.
的最小值是_________.
(3)结合函数图象,当![]() 时,求x的取值范围.
时,求x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,点![]() 是
是![]() 轴上一点,其坐标为
轴上一点,其坐标为![]() ,点
,点![]() 在
在![]() 轴的正半轴上.点
轴的正半轴上.点![]() ,
,![]() 均在线段
均在线段![]() 上,点
上,点![]() 的横坐标为
的横坐标为![]() ,点
,点![]() 的横坐标大于
的横坐标大于![]() ,在
,在![]() 中,若
中,若![]() 轴,
轴,![]() 轴, 则称
轴, 则称![]() 为点
为点![]() ,
,![]() 的“肩三角形.
的“肩三角形.
(1)若点![]() 坐标为
坐标为![]() , 且
, 且![]() ,则点
,则点![]() ,
,![]() 的“肩三角形”的面积为__ ;
的“肩三角形”的面积为__ ;
(2)当点![]() ,
,![]() 的“肩三角形”是等腰三角形时,求点
的“肩三角形”是等腰三角形时,求点![]() 的坐标;
的坐标;
(3)在(2)的条件下,作过![]() ,
,![]() ,
,![]() 三点的抛物线
三点的抛物线![]() .
.
①若![]() 点必为抛物线上一点,求点
点必为抛物线上一点,求点![]() ,
,![]() 的“肩三角形”面积
的“肩三角形”面积![]() 与
与![]() 之间的函数关系式,并写出自变量
之间的函数关系式,并写出自变量![]() 的取值范围.
的取值范围.
②当点![]() ,
,![]() 的“肩三角形”面积为3,且抛物线
的“肩三角形”面积为3,且抛物线![]() 与点
与点![]() ,
,![]() 的“肩三角形”恰有两个交点时,直接写出
的“肩三角形”恰有两个交点时,直接写出![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
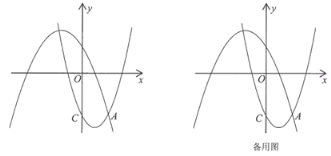
【题目】如图,在平面直角坐标系xOy中,抛物线L1:![]() 过点C(0,﹣3),与抛物线L2:
过点C(0,﹣3),与抛物线L2:![]() 的一个交点为A,且点A的横坐标为2,点P、Q分别是抛物线L1、抛物线L2上的动点.
的一个交点为A,且点A的横坐标为2,点P、Q分别是抛物线L1、抛物线L2上的动点.
(1)求抛物线L1对应的函数表达式;
(2)若以点A、C、P、Q为顶点的四边形恰为平行四边形,求出点P的坐标;
(3)设点R为抛物线L1上另一个动点,且CA平分∠PCR,若OQ∥PR,求出点Q的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com