
【题目】有一块锐角三角形卡纸余料ABC,它的边BC=120cm,高AD=80cm,为使卡纸余料得到充分利用,现把它裁剪成一个邻边之比为2:5的矩形纸片EFGH和正方形纸片PMNQ,裁剪时,矩形纸片的较长边在BC上,正方形纸片一边在矩形纸片的较长边EH上,其余顶点均分别在AB,AC上,具体裁剪方式如图所示。
(1)求矩形纸片较长边EH的长;
(2)裁剪正方形纸片时,小聪同学是按以下方法进行裁剪的:先沿着剩余料![]() 中与边EH平行的中位线剪一刀,再沿过该中位线两端点向边EH所作的垂线剪两刀,请你通过计算,判断小聪的剪法是否正确.
中与边EH平行的中位线剪一刀,再沿过该中位线两端点向边EH所作的垂线剪两刀,请你通过计算,判断小聪的剪法是否正确.

科目:初中数学 来源: 题型:
【题目】已知抛物线y=ax2﹣8ax+12a(a<0)与x轴交于A、B两点(点A在点B的左边),抛物线上另有一点C在第一象限,且使△OCA∽△OBC,
(1)求OC的长及![]() 的值;
的值;
(2)设直线BC与y轴交于P点,当点C恰好在OP的垂直平分线上时,求直线BP和抛物线的解析式.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等腰三角形 ABC 中,AC=BC=13,AB=10.以 BC 为直径作⊙O 交 AB 于点 D,交 AC 于点 G,DF⊥AC,垂足为 F,交 CB 的延长线于点 E.
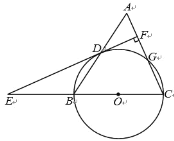
(1)求证:直线 EF 是⊙O 的切线;
(2)求 sin∠E 的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 和
和![]() 都是等腰直角三角形,
都是等腰直角三角形,![]() ,
,![]() 的顶点
的顶点![]() 与
与![]() 的斜边
的斜边![]() 的中点重合,将
的中点重合,将![]() 绕点
绕点![]() 旋转,旋转过程中,线段
旋转,旋转过程中,线段![]() 与线段
与线段![]() 相交于点
相交于点![]() ,射线
,射线![]() 与线段
与线段![]() 相交于点
相交于点![]() ,与射线
,与射线![]() 相交于点
相交于点![]() .
.
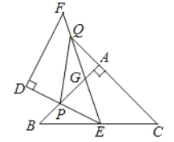
(1)求证:![]() ;
;
(2)求证:![]() 平分
平分![]() ;
;
(3)当![]() ,
,![]() ,求
,求![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,用长为22米的篱笆,一面利用墙(墙的最大可用长度为14米),围成中间隔有一道篱笆的长方形花圃,为了方便出入,在建造篱笆花圃时,在BC上用其他材料做了宽为1米的两扇小门.
(1)设花圃的一边AB长为x米,请你用含x的代数式表示另一边AD的长为 米;
(2)若此时花圃的面积刚好为45m2,求此时花圃的长与宽.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线,![]() 与
与![]() 轴交于
轴交于![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() ,且抛物线
,且抛物线![]() 的对称轴为直线
的对称轴为直线![]() .
.
(1)抛物线的表达式;
(2)若抛物线![]() 与抛物线
与抛物线![]() 关于直线
关于直线![]() 对称,抛物线
对称,抛物线![]() 与
与![]() 轴交于点
轴交于点![]() 两点(点
两点(点![]() 在点
在点![]() 左侧),要使
左侧),要使![]() ,求所有满足条件的抛物线
,求所有满足条件的抛物线![]() 的表达式.
的表达式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将一个矩形纸片OABC放置在平面直角坐标系xOy内,点A(6,0),点C(0,4),点O(0,0).点P是线段BC上的动点,将△OCP沿OP翻折得到△OC′P.

(Ⅰ)如图①,当点C′落在线段AP上时,求点P的坐标;
(Ⅱ)如图②,当点P为线段BC中点时,求线段BC′的长度.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com