
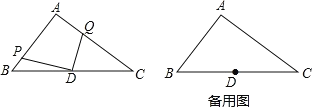
【题目】如图,在Rt△ABC中,∠BAC=90,AB=6,AC=8,点D为边BC的中点,点P为射线AB上的一动点,点Q为边AC上的一动点,且∠PDQ=90.
(1)当DP⊥AB时,求CQ的长;
(2)当BP=2,求CQ的长;
(3)连结AD,若AD平分∠PDQ,求DP:DQ.
【答案】(1)4;(2)CQ的长为![]() 或
或![]() ;(3)4:3;
;(3)4:3;
【解析】
(1)首先证明DQ∥AB,根据平行线等分线段定理即可解决问题.
(2)分情况讨论,①中,当点P在线段AB上时,作DM⊥AB,DN⊥AC,由相似推出QN=![]() ,推出PM=BM-PB=1,再推出QN=
,推出PM=BM-PB=1,再推出QN=![]() ;②中,当点P在AB的延长线上,根据PM,QN的值,CQ=QN+CN计算即可.
;②中,当点P在AB的延长线上,根据PM,QN的值,CQ=QN+CN计算即可.
(3)首先证明四边形AMDN是正方形,由全等推出PM=NQ,推出PD+DQ的值,再由(2)结论即可计算.
(1)如图1中,
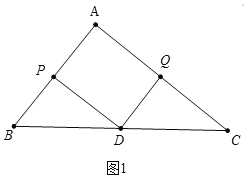
∵DP⊥AB,DQ⊥DP,
∴DQ∥AB,
∵BD=DC,
∴CQ=AQ=4.
(2)①如图2中,当点P在线段AB上时,作DM⊥AB,DN⊥AC,垂足分别为M、N,
则四边形AMDN是矩形,DM、DN分别是△ABC的中位线,DM=4,DN=3,
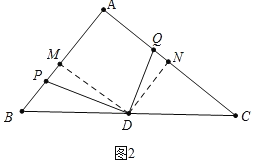
∵∠PDQ=∠MDN=90°,
∴∠PDM=∠QDN,∵∠DNQ∠DMP=90°,
∴△PDM∽△QDN,
∴![]() =
= ![]() =
=![]() ,
,
∴QN=![]() PM,
PM,
∵PM=BMPB=32=1,
∴QN=![]() ,
,
∴CQ=QN+CN=![]() +4=
+4=![]() .
.
②如图3中,当点P在AB的延长线上时,PM=5,QN=![]() ,CQ=QN+CN=4+
,CQ=QN+CN=4+![]() =
=![]() ,
,
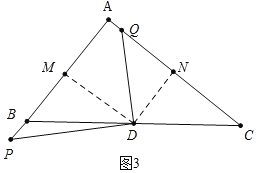
综上所述,当BP=2,求CQ的长为![]() 或
或![]() .
.
(3)如图4中,作AM⊥DP于M,AN⊥DQ于N.
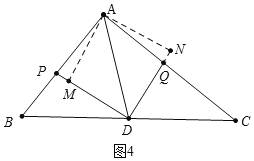
∵AD平分∠PDQ,
∴AM=AN,
∵∠AMD=∠AND=∠MDN=90,
∴四边形AMDN是矩形,∵AM=AN,
∴四边形AMDN是正方形,
∴∠MAN=90,DM=DN,
∵∠BAC=∠MAN=90,
∴∠PAM=∠NAQ,
∴△APM≌△AQN,
∴PM=NQ,
∵AB=6,AC=8,
∴BC=![]() =10,AD=5,
=10,AD=5,
∵PD+DQ=(PM+MD)+(DNQN)=2DM=![]() AD=
AD=![]() ,
,
由(2)可知PD:QD=4:3,


 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案科目:初中数学 来源: 题型:
【题目】如图,在边长为1的正方形网格中,两个三角形的顶点都在格点(网线的交点)上,下列方案中不能把△ABC平移至△DEF位置的是( )
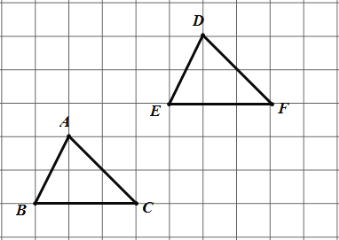
A.先把△ABC沿水平方向向右平移4个单位长度,再向上平移3个单位长度
B.先把△ABC向上平移3个单位长度,再沿水平方向向右平移4个单位长度
C.把△ABC沿BE方向移动5个单位长度
D.把△ABC沿BE方向移动6个单位长度
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在边长为2的正方形ABCD中,P为AB上的一动点,E为AD中点,FE交CD延长线于Q,过E作EF⊥PQ交BC的延长线于F,则下列结论:①△APE≌△DQE;②PQ=EF;③当P为AB中点时,CF=![]() ;④若H为QC的中点,当P从A移动到B时,线段EH扫过的面积为
;④若H为QC的中点,当P从A移动到B时,线段EH扫过的面积为![]() ,其中正确的是( )
,其中正确的是( )
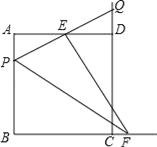
A. ①② B. ①②④ C. ②③④ D. ①②③
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法中错误的是【 】
A.某种彩票的中奖率为1%,买100张彩票一定有1张中奖
B.从装有10个红球的袋子中,摸出1个白球是不可能事件
C.为了解一批日光灯的使用寿命,可采用抽样调查的方式
D.掷一枚普通的正六面体骰子,出现向上一面点数是2的概率是![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在Rt△ACB中,∠ACB=90°,AC=BC,D为AB上一点,连结CD,将CD绕C点逆时针旋转90°至CE,连结DE,过C作CF⊥DE交AB于F,连结BE.
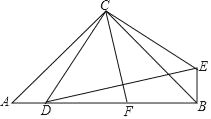
(1)求证:AD=BE;
(2)求证:AD2+BF2=DF2;
(3)若∠ACD=15°,CD=![]() +1,求BF.
+1,求BF.
查看答案和解析>>
科目:初中数学 来源: 题型:
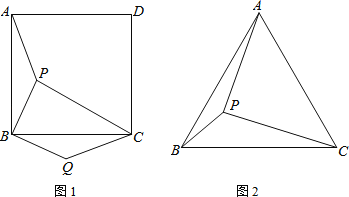
【题目】(1)如图1,点P是正方形ABCD内的一点,把△ABP绕点B顺时针方向旋转,使点A与点C重合,点P的对应点是Q.若PA=3,PB=2![]() ,PC=5,求∠BQC的度数.
,PC=5,求∠BQC的度数.
(2)点P是等边三角形ABC内的一点,若PA=12,PB=5,PC=13,求∠BPA的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,设二次函数y=ax2﹣4ax,其中为常数且a<0.
(1)若函数y=ax2﹣4ax的图象经过点(2,4),求此函数表达式;
(2)若抛物线y=ax2﹣4ax的顶点在双曲线![]() 上,试说明k的符号;
上,试说明k的符号;
(3)已知(m,y1)、(m+1,y2)、(m+2,y3),(0<m<1)都是抛物线y=ax2﹣4ax(a<0)上的点,请判断y1,y2,y3的大小,并说明理由﹒
查看答案和解析>>
科目:初中数学 来源: 题型:
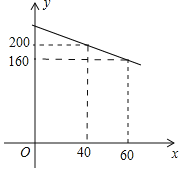
【题目】某厂家生产一种新型电子产品,制造时每件的成本为40元,通过试销发现,销售量![]() 万件
万件![]() 与销售单价
与销售单价![]() 元
元![]() 之间符合一次函数关系,其图象如图所示.
之间符合一次函数关系,其图象如图所示.
![]() 求y与x的函数关系式;
求y与x的函数关系式;
![]() 物价部门规定:这种电子产品销售单价不得超过每件80元,那么,当销售单价x定为每件多少元时,厂家每月获得的利润
物价部门规定:这种电子产品销售单价不得超过每件80元,那么,当销售单价x定为每件多少元时,厂家每月获得的利润![]() 最大?最大利润是多少?
最大?最大利润是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com