练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，把原来弯曲的河道改直，A，B两地间的河道长度变短，这样做的道理是（　　）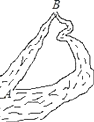

    A.两点确定一条直线
    B.两点之间线段最短
    C.两点之间直线最短
    D.垂线段最短

    【答案】B
    【解析】A、图中AB属于线段关系，A不符合题意；
    B、图中AB属于线段关系，且关于线段之间的距离从弯曲的改为直的，B符合题意；
    C、图中AB属于线段关系，C不符合题意；
    D、垂线段最短是指点到直线的距离，图中是点与点之间的距离，D不符合题意。
    所以答案是B。


    【考点精析】本题主要考查了线段的基本性质和两点间的距离的相关知识点，需要掌握线段公理：所有连接两点的线中，线段最短．也可简单说成：两点之间线段最短；连接两点的线段的长度，叫做这两点的距离；线段的大小关系和它们的长度的大小关系是一致的；同轴两点求距离，大减小数就为之．与轴等距两个点，间距求法亦如此．平面任意两个点，横纵标差先求值．差方相加开平方，距离公式要牢记才能正确解答此题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图，C为半圆内一点，O为圆心，直径AB长为2cm，∠BOC=60°，∠BCO=90°，将△BOC绕圆心O逆时针旋转至△B′OC′，点C′在OA上，则边BC扫过区域（图中阴影部分）的面积为 cm2．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】昆明在修建地铁3号线的过程中，要打通隧道3600米，为加快城市建设，实际工作效率是原计划工作效率的1.8倍，结果提前20天完成了任务．问原计划每天打通隧道多少米？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在证明“△ABC内角和等于180°”时，延长BC至D，过点C作CE∥AB，得到∠ABC=∠ECD，∠BAC=∠ACE，由于∠BCD=180°，可得到∠ABC+∠ACB+∠BAC=180°，这个证明方法体现的数学思想是（ ）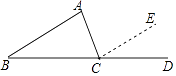
    A.数形结合
    B.特殊到一般
    C.一般到特殊
    D.转化

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，已知抛物线（a≠0）交x轴与A，B两点（点A在点B左侧），将直尺WXYZ与x轴负方向成45°放置，边WZ经过抛物线上的点C（4，m），与抛物线的另一交点为点D，直尺被x轴截得的线段EF=2，且△CEF的面积为6．

    （1）求该抛物线的解析式；

    （2）探究：在直线AC上方的抛物线上是否存在一点P，使得△ACP的面积最大？若存在，请求出面积的最大值及此时点P的坐标；若不存在，请说明理由．

    （3）将直尺以每秒2个单位的速度沿x轴向左平移，设平移的时间为t秒，平移后的直尺为W′X′Y′Z′，其中边X′Y′所在的直线与x轴交于点M，与抛物线的其中一个交点为点N，请直接写出当t为何值时，可使得以C、D、M、N为顶点的四边形是平行四边形．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在正方形ABCD中，点A在y轴正半轴上，点B的坐标为（0，﹣3），反比例函数y=﹣的图象经过点C．
    （1）求点C的坐标；
    （2）若点P是反比例函数图象上的一点且S△PAD=S正方形ABCD；求点P的坐标．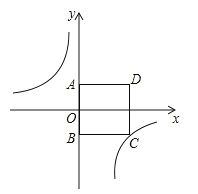

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】图①是我们常见的地砖上的图案，其中包含了一种特殊的平面图形﹣正八边形．

    （1）如图②，AE是⊙O的直径，用直尺和圆规作⊙O的内接正八边形ABCDEFGH（不写作法，保留作图痕迹）；

    （2）在（1）的前提下，连接OD，已知OA=5，若扇形OAD（∠AOD＜180°）是一个圆锥的侧面，则这个圆锥底面圆的半径等于 ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】列方程解应用题 某商店用2000元购进一批小学生书包，出售后发现供不应求，商店又购进第二批同样的书包，所购数量是第一批购进数量的3倍，但单价贵了2元，结果购买第二批书包用了6600元．
    （1）请求出第一批每只书包的进价；
    （2）该商店第一批和第二批分别购进了多少只书包；
    （3）若商店销售这两批书包时，每个售价都是30元，全部售出后，商店共盈利多少元？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】要反映我区12月11日至17日这一周每天的最高气温的变化趋势，宜采用（　　）

    A. 条形统计图 B. 折线统计图

    C. 扇形统计图 D. 频数分布统计图

    查看答案和解析>>

    同步练习册答案