
【题目】如图,在证明“△ABC内角和等于180°”时,延长BC至D,过点C作CE∥AB,得到∠ABC=∠ECD,∠BAC=∠ACE,由于∠BCD=180°,可得到∠ABC+∠ACB+∠BAC=180°,这个证明方法体现的数学思想是( ) 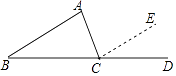
A.数形结合
B.特殊到一般
C.一般到特殊
D.转化
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
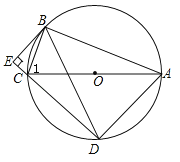
【题目】如图,⊙O是△ABC的外接圆,AC为直径,弦BD=BA,BE⊥DC交DC的延长线于点E,求证:
(1)∠1=∠BAD;
(2)BE是⊙O的切线.
查看答案和解析>>
科目:初中数学 来源: 题型:
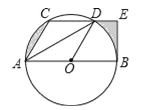
【题目】如图,CD是⊙O的弦,AB是直径,且CD∥AB,连接AC、AD、OD,其中AC=CD,过点B的切线交CD的延长线于E.
(1)求证:DA平分∠CDO;
(2)若AB=12,求图中阴影部分的周长之和(参考数据:π=3.1,![]() =1.4,
=1.4,![]() =1.7).
=1.7).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,把△ABC向上平移4个的那位长度,再向右平移3个单位长度,得到△A′B′C′.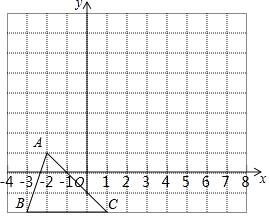
(1)在图中画出△A′B′C′;
(2)连接A′A、C′C,求四边形A′AC′C的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,把原来弯曲的河道改直,A,B两地间的河道长度变短,这样做的道理是( )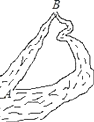
A.两点确定一条直线
B.两点之间线段最短
C.两点之间直线最短
D.垂线段最短
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】按一定规律排列的一列数:21 , 22 , 23 , 25 , 28 , 213 , …,若x、y、z表示这列数中的连续三个数,猜想x、y、z满足的关系式是 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com