
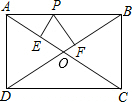
 在矩形ABCD中,P为AB上的动点,PE⊥AC于E,PF⊥BD于F,求证:PE+PF为定值.
在矩形ABCD中,P为AB上的动点,PE⊥AC于E,PF⊥BD于F,求证:PE+PF为定值. 解:∵四边形ABCD是矩形,
解:∵四边形ABCD是矩形,| PF |
| BC |
| BP |
| BD |
| BP•BC |
| BD |
| PE |
| AD |
| AP |
| CA |
| AP•AD |
| CA |
| BP•BC |
| BD |
| AP•AD |
| CA |
| BP•BC+AP•AD |
| BD |
| (BP+AP)•BC |
| BD |
| AB•BC |
| BD |
| AB•BC |
| BD |


科目:初中数学 来源: 题型:
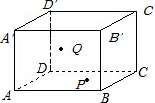 如图是一个长方体形空水池,AB=10m,BC=5m,BB′=6m,在内壁ABB′A′的P处(点P到AB和BB′的距离都为1m)有一只壁虎,它想去吃在内壁CDD′C′上的Q处(点Q到CD和DD′的距离都为3m)的苍蝇,求它从点P爬到点Q的最短路径的长度.
如图是一个长方体形空水池,AB=10m,BC=5m,BB′=6m,在内壁ABB′A′的P处(点P到AB和BB′的距离都为1m)有一只壁虎,它想去吃在内壁CDD′C′上的Q处(点Q到CD和DD′的距离都为3m)的苍蝇,求它从点P爬到点Q的最短路径的长度.查看答案和解析>>
科目:初中数学 来源: 题型:
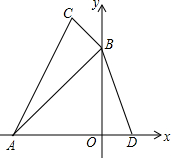 如图,在平面直角坐标系中,△ABC中点A(-3,0),B(0,3),C(-1,4),在x轴正半轴中有一个点D(1,0),连结BD,问:
如图,在平面直角坐标系中,△ABC中点A(-3,0),B(0,3),C(-1,4),在x轴正半轴中有一个点D(1,0),连结BD,问:查看答案和解析>>
科目:初中数学 来源: 题型:
 在一张城市地图上,有学校、医院、图书馆三地,但被墨迹污染,图书馆的具体位置看不清,但知道图书馆在学校的东北方向,在医院的南偏西75°方向,你能确定图书馆的位置吗?
在一张城市地图上,有学校、医院、图书馆三地,但被墨迹污染,图书馆的具体位置看不清,但知道图书馆在学校的东北方向,在医院的南偏西75°方向,你能确定图书馆的位置吗?查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com