
一个不透明的布袋里装有4个兵乓球,每个求上面分别标有1、2、3、4,从布袋中随机摸取一个兵乓球,记下数字
(1)若将第一次摸取的兵乓球放回后,摇匀,再随机摸取第二个兵乓球,记下数字
①请你用树状图或列表法列出所有可能的结果;
②求“两次记下的数字之和大于4且小于7”的概率;
(2)若将第一次摸取的兵乓球记下数字后不放回,再随机摸取第二个兵乓球并记下数字,请直接写出“两次记下的数字之和大于4且小于7”的概率.
【考点】列表法与树状图法.
【分析】(1)根据概率的求法,找准两点:①全部情况的总数;②符合条件的情况数目;二者的比值就是其发生的概率.使用列表法分析时,一定要做到不重不漏.
(2)依据题意先用列表法或画树状图法分析所有等可能和达到某种效果的可能,然后根据概率公式求出该事件的概率.
【解答】解:(1)①列表如下,
|
| 1 | 2 | 3 | 4 |
| 1 | 1,1 | 1,2 | 1,3 | 1,4 |
| 2 | 2,1 | 2,2 | 2,3 | 2,4 |
| 3 | 3,1 | 3,2 | 3,3 | 3,4 |
| 4 | 4,1 | 4,2 | 4,3 | 4,4 |
②∵由表可知,共有16个等可能的结果,“两次记下的数字之和大于4且小于7”的有7次,
∴P(两次记下的数字之和大于4且小于7)=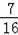
 ;
;
(2)根据题意画树形图如下:
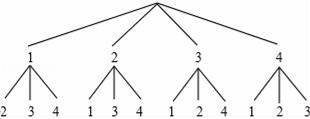

由以上可知共有12种可能结果分别为:(1,2),(1,3),(1,4),(2,1),(2,3),(2,4),(3,1),(3,2),(3,4),(4,1),(4,2),(4,3);“两次记下的数字之和大于4且小于7”的有(1,4),(2,3),(2,4),(3,2),(4,1),(4,2)6种,
故P(两次记下的数字之和大于4且小于7)=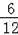
 =
=
 ;.
;.
【点评】此题考查的是用列表法或树状图法求概率.列表法可以不重复不遗漏的列出所有可能的结果,适合于两步完成的事件;树状图法适合两步或两步以上完成的事件;用到的知识点为:概率=所求情况数与总情况数之比.


科目:初中数学 来源: 题型:
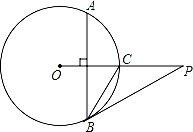
如图,已知点P是⊙O外一点,PO交圆O于点C,OC=2,AB⊥OC,劣弧AB的度数为120°,连接PB.
(1)求征:OC=BC;
(2)当PB的长是多少时,PB是⊙O的切线?写出证明过程.
查看答案和解析>>
科目:初中数学 来源: 题型:
某车的刹车距离y(m)与开始刹车时的速度x(m/s)之间满足二次函数y=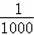
 x2+
x2+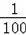
 x(x>0),若该车某次的刹车距离为9m,则开始刹车时的速度为 m/s.
x(x>0),若该车某次的刹车距离为9m,则开始刹车时的速度为 m/s.
查看答案和解析>>
科目:初中数学 来源: 题型:
一辆慢车与一辆快车分别从甲、乙两地同时出发,匀速相向而行,两车在途中相遇后都停留一段时间,然后分别按原速一同驶往甲地后停车.设慢车行驶的时间为x小时,两车之间的距离为y千米,图中折线表示y与x之间的函数图象.当快车到达甲地时,慢车离甲地的距离为 千米.
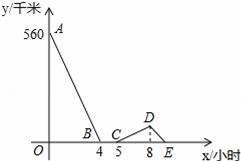

查看答案和解析>>
科目:初中数学 来源: 题型:
如图1,动直线l:y=kx+2交抛物线y=
 x2于A、B两点(A在B的左边),交y轴于M点,N为x轴正半轴上一点,且ON=OM+1
x2于A、B两点(A在B的左边),交y轴于M点,N为x轴正半轴上一点,且ON=OM+1
(1)直接写出M、N两点的坐标
(2)如图1,连AN、BN,当∠ANB=90°时,求k的值;如图2,过B作y轴的平行线交直线OA于C,试探求△MNC的周长的最小值.
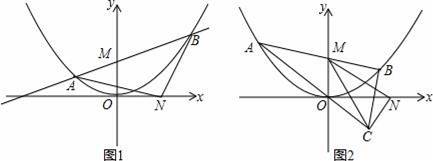

查看答案和解析>>
科目:初中数学 来源: 题型:
在学校的艺术节上为了表彰在书法比赛中成绩突出的学生,购买了钢笔30支,毛笔45支,共用了1755元,其中每支毛笔比钢笔贵4元。求钢笔和毛笔 的单价各为多少元?(8分)
的单价各为多少元?(8分)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com