
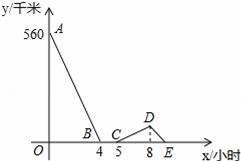
一辆慢车与一辆快车分别从甲、乙两地同时出发,匀速相向而行,两车在途中相遇后都停留一段时间,然后分别按原速一同驶往甲地后停车.设慢车行驶的时间为x小时,两车之间的距离为y千米,图中折线表示y与x之间的函数图象.当快车到达甲地时,慢车离甲地的距离为 千米.

60 千米.
【考点】一次函数的应用.
【分析】先根据题意得出慢车往返分别用了4小时,慢车行驶4小时的距离,快车3小时即可行驶完,进而求出快车速度以及利用两车速度之比得出慢车速度;再求出快车到达甲地用时,即可求出快车到达甲地时慢车据甲地的距离.
【解答】解:由题意可得出:慢车和快车经过4个小时后相遇,相遇后停留了1个小时,出发后两车之间的距离开始增大,快车到达甲地后两车之间的距离开始缩小,由图分析可知快车经过3个小时后到达甲地,此段路程慢车需要行驶4小时,因此慢车和快车的速度之比为3:4,
∴设慢车速度为3xkm/h,快车速度为4xkm/h,
∴(3x+4x)×4=560,x=20,
∴快车的速度是80km/h,慢车的速度是60km/h.
快车和慢车相遇地离甲地的距离为4×60=240km,
当慢车行驶了7小时后,快车已到达甲地,此时两车之间的距离为240﹣3×60=60km.
故答案为60.
【点评】本题主要考查的是函数图象的应用,根据图象得出相应的信息是解题的关键.


科目:初中数学 来源: 题型:
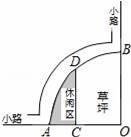
如图是某公园的一角,∠AOB=90°,弧AB的半径OA长是6米,C是OA的中点,点D在弧AB上,CD∥OB,则图中休闲区(阴影部分)的面积是( )

A.(10π﹣
 )米2 B.(π﹣
)米2 B.(π﹣
 )米2 C.(6π﹣
)米2 C.(6π﹣
 )米2 D.(6π﹣
)米2 D.(6π﹣
 )米2
)米2
查看答案和解析>>
科目:初中数学 来源: 题型:
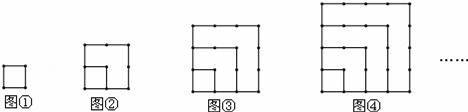
用火柴棍按下列方式摆图形,第1个图形用了4根火柴棍,第2个图形用了10根火柴棍,第3个图形用了18根火柴棍.依照此规律,若第n个图形用了88根火柴棍,则n的值为( )

A.6 B.7 C.8 D.9
查看答案和解析>>
科目:初中数学 来源: 题型:
一个不透明的布袋里装有4个兵乓球,每个求上面分别标有1、2、3、4,从布袋中随机摸取一个兵乓球,记下数字
(1)若将第一次摸取的兵乓球放回后,摇匀,再随机摸取第二个兵乓球,记下数字
①请你用树状图或列表法列出所有可能的结果;
②求“两次记下的数字之和大于4且小于7”的概率;
(2)若将第一次摸取的兵乓球记下数字后不放回,再随机摸取第二个兵乓球并记下数字,请直接写出“两次记下的数字之和大于4且小于7”的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com