

 时,求PE及DH的长。
时,求PE及DH的长。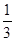 。
。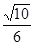 , DH=
, DH=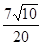 。
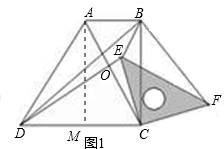
。
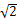 .
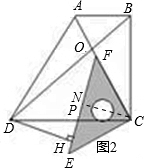
.
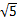 ,
,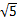 /3,
/3,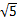 /3-
/3-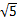 /6=
/6=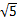 /2,
/2,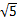 /2:2=CP:2
/2:2=CP:2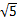 /3,
/3,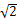 ,BO:DO=1:2,
,BO:DO=1:2,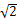 /3,
/3,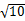 /3,PE=
/3,PE=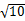 /6。
/6。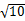 /20。
/20。

科目:初中数学 来源:不详 题型:单选题
| A.10米 | B.15米 | C.25米 | D.30米 |

查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 长的直线型通道,中国馆位于世博轴的一侧(如下图所示). 现测得中国馆到世博轴两端的距离相等,并且从中国馆看世博轴两端的视角为
长的直线型通道,中国馆位于世博轴的一侧(如下图所示). 现测得中国馆到世博轴两端的距离相等,并且从中国馆看世博轴两端的视角为 . 据此数据计算,求:中国馆到世博轴其中一端的距离是多少?.
. 据此数据计算,求:中国馆到世博轴其中一端的距离是多少?.
|
查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
 ,那么A、B两点的距离为( )
,那么A、B两点的距离为( )  , B .a·tan
, B .a·tan C. a·cos
C. a·cos D .
D . 

查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 ≈1.73).
≈1.73).
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题


查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com