
°æƒø°ø»ÁÕº£¨‘⁄![]() ÷–£¨
÷–£¨![]() £¨
£¨![]() £Æ∂ص„
£Æ∂ص„![]() ¥”µ„
¥”µ„![]() ≥ˆ∑¢£¨—ÿ
≥ˆ∑¢£¨—ÿ![]() “‘√ø√Î
“‘√ø√Î![]() ∏ˆµ•Œª≥§∂»µƒÀŸ∂»œÚ÷’µ„
∏ˆµ•Œª≥§∂»µƒÀŸ∂»œÚ÷’µ„![]() ‘À∂Ø£¨µ±µ„
‘À∂Ø£¨µ±µ„![]() ”ε„
”ε„![]() °¢
°¢![]() ≤ª÷ÿ∫œ ±£¨π˝µ„
≤ª÷ÿ∫œ ±£¨π˝µ„![]() ◊˜
◊˜![]() Ωª’€œþ
Ωª’€œþ![]() ”⁄µ„
”⁄µ„![]() £¨“‘
£¨“‘![]() Œ™±þœÚ◊Û◊˜’˝∑Ω–Œ
Œ™±þœÚ◊Û◊˜’˝∑Ω–Œ![]() £Æ…Ë’˝∑Ω–Œ
£Æ…Ë’˝∑Ω–Œ![]() ”Î
”Î![]() ÷ÿµ˛≤ø∑÷Õº–Œµƒ√ʪ˝Œ™
÷ÿµ˛≤ø∑÷Õº–Œµƒ√ʪ˝Œ™![]() £®∆Ω∑Ωµ•Œª£©£¨µ„
£®∆Ω∑Ωµ•Œª£©£¨µ„![]() ‘À∂صƒ ±º‰Œ™
‘À∂صƒ ±º‰Œ™![]() £®√Σ©£Æ
£®√Σ©£Æ
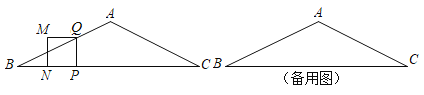
°°°°°°°° ±∏”√Õº
£®1£©”√∫¨![]() µƒ¥˙ ˝ Ω±Ì æ
µƒ¥˙ ˝ Ω±Ì æ![]() µƒ≥§£Æ
µƒ≥§£Æ
£®2£©÷±Ω”–¥≥ˆµ„![]() ‘⁄
‘⁄![]() ƒ⁄≤ø ±
ƒ⁄≤ø ±![]() µƒ»°÷µ∑∂Œß£Æ
µƒ»°÷µ∑∂Œß£Æ
£®3£©«Û![]() ”Î
”Î![]() ÷ƺ‰µƒ∫Ø ˝πÿœµ Ω£Æ
÷ƺ‰µƒ∫Ø ˝πÿœµ Ω£Æ
£®4£©÷±Ω”–¥≥ˆµ„![]() ¬‰‘⁄
¬‰‘⁄![]() µƒ÷–ŒªœþÀ˘‘⁄÷±œþ…œ ±
µƒ÷–ŒªœþÀ˘‘⁄÷±œþ…œ ±![]() µƒ÷µ£Æ
µƒ÷µ£Æ
°æ¥∞∏°ø£®1£©PQ=![]() £ª£®2£©
£ª£®2£©![]() £ª£®3£©µ±
£ª£®3£©µ±![]() ±£¨
±£¨![]() £ªµ±
£ªµ±![]() ±£¨
±£¨![]() £ªµ±
£ªµ±![]() ±£¨
±£¨![]() £ª£®4£©
£ª£®4£©![]() £¨
£¨![]() £¨
£¨![]() £¨
£¨![]() £Æ
£Æ
°æΩ‚Œˆ°ø
£®1£©∑÷¡Ω÷÷«ÈøˆÃ÷¬€:µ±µ„Q‘⁄œþ∂ŒAB…œ ±,µ±µ„Q‘⁄œþ∂ŒAC…œ ±;
£®2£©œ»º∆À„M‘⁄±þAB…œ ±tµƒ÷µ,∏˘æðµ„M‘⁄°˜ABCƒ⁄≤ø ±¡Ω∏ˆ±þΩÁµ„º¥ø…Ω‚¥;
£®3£©∑÷»˝÷÷«Èøˆ:
¢Ÿ0£ºt°Ð1 ±,’˝∑Ω–ŒPQMN”ΰ˜ABC÷ÿµ˛≤ø∑÷Õº–Œ «Àƒ±þ–ŒDNPQ,
¢⁄µ±1£ºt£º![]() ±,’˝∑Ω–ŒPQMN”ΰ˜ABC÷ÿµ˛≤ø∑÷Õº–Œ «ŒÂ±þ–ŒODNPQ,
±,’˝∑Ω–ŒPQMN”ΰ˜ABC÷ÿµ˛≤ø∑÷Õº–Œ «ŒÂ±þ–ŒODNPQ,
¢€µ±![]() °Ðt£º2 ±,’˝∑Ω–ŒPQMN”ΰ˜ABC÷ÿµ˛≤ø∑÷Õº–Œ «’˝∑Ω–ŒMNPQ,
°Ðt£º2 ±,’˝∑Ω–ŒPQMN”ΰ˜ABC÷ÿµ˛≤ø∑÷Õº–Œ «’˝∑Ω–ŒMNPQ,
∑÷±º∆À„√ʪ˝º¥ø…;
£®4£©µ„M¬‰‘⁄°˜ABCµƒ÷–ŒªœþÀ˘‘⁄÷±œþ…œ ±,¥Ê‘⁄Àƒ÷÷«Èøˆ,ª≠Õºø…Ω‚¥£Æ
Ω‚:£®1£©”…“‚µ√:BP£Ω2t,
»ÁÕº1,π˝A◊˜AD°ÕBC”⁄D,
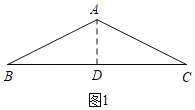
°þAB£ΩAC£Ω![]() ,BC£Ω4,
,BC£Ω4,
°ýBD£ΩCD£Ω![]() BC£Ω2£¨
BC£Ω2£¨
°ýAD£Ω![]() ,
,
°ýtan°œB£Ω![]() £Ω
£Ω![]() ,
,
∑÷¡Ω÷÷«Èøˆ:
¢Ÿµ±µ„Q‘⁄œþ∂ŒAB…œ ±,º¥0£ºt°Ð1 ±,»ÁÕº2,
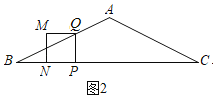
°ýtan°œB£Ω![]() ,
,
°ýPQ£Ωt;
¢⁄µ±µ„Q‘⁄œþ∂ŒAC…œ ±,º¥1£ºt£º2 ±,»ÁÕº3,
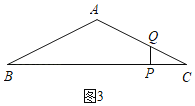
°ýtan°œC£Ωtan°œB£Ω![]() £Ω
£Ω![]() ,
,
°ýPQ£Ω![]() PC£Ω
PC£Ω![]() £Ω2©Åt;
£Ω2©Åt;
£®2£©µ±M‘⁄±þAB…œ ±,»ÁÕº4,
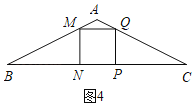
”…£®1£©÷™:MN£ΩPQ£Ω2©Åt£ΩPN,
tan°œB£Ω![]() £Ω
£Ω![]() ,
,
°ýBN£Ω2MN,
°þBP£ΩBN+PN,
°ý2t£Ω3MN£Ω3£®2©Åt£©,
t£Ω![]() ,
,
°ýµ„M‘⁄°˜ABCƒ⁄≤ø ±tµƒ»°÷µ∑∂Œß «![]() £ºt£º2;
£ºt£º2;
£®3£©∑÷»˝÷÷«Èøˆ:
¢Ÿ0£ºt°Ð1 ±,»ÁÕº5,’˝∑Ω–ŒPQMN”ΰ˜ABC÷ÿµ˛≤ø∑÷Õº–Œ «Àƒ±þ–ŒDNPQ,
BP£Ω2t,PQ£ΩPN£ΩMD£Ωt,
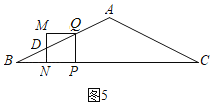
°ýBN£Ω2t©Åt£Ωt,
°ýDN£Ω![]() t£ΩDM,
t£ΩDM,
°ýS£ΩS’˝∑Ω–ŒMNPQ©ÅS°˜MDQ£Ω![]() ;
;
¢⁄µ±1£ºt£º![]() ±,»ÁÕº6,’˝∑Ω–ŒPQMN”ΰ˜ABC÷ÿµ˛≤ø∑÷Õº–Œ «ŒÂ±þ–ŒODNPQ,
±,»ÁÕº6,’˝∑Ω–ŒPQMN”ΰ˜ABC÷ÿµ˛≤ø∑÷Õº–Œ «ŒÂ±þ–ŒODNPQ,
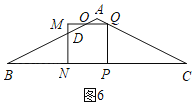
°þPQ£ΩPN£ΩMN£Ω2©Åt,
°ýBN£ΩBP©ÅPN£Ω2t©Å£®2©Åt£©£Ω3t©Å2,
°þtan°œB£Ω![]() ,DN£Ω
,DN£Ω![]() BN£Ω
BN£Ω![]() ,
,
°ýDM£ΩMN©ÅDN£Ω2©Åt©Å![]() £Ω3©Å
£Ω3©Å![]() t,
t,
°þtan°œMOD£Ωtan°œB£Ω![]() £Ω
£Ω![]() ,
,
°ýOM£Ω2MD,
°ýS£ΩS’˝∑Ω–ŒMNPQ©ÅS°˜MDO£Ω£®2©Åt£©2©Å![]() £Ω£®2©Åt£©2©Å
£Ω£®2©Åt£©2©Å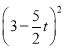 £Ω©Å
£Ω©Å![]() +11t©Å5;
+11t©Å5;
¢€µ±![]() °Ðt£º2 ±,»ÁÕº7,’˝∑Ω–ŒPQMN”ΰ˜ABC÷ÿµ˛≤ø∑÷Õº–Œ «’˝∑Ω–ŒMNPQ,
°Ðt£º2 ±,»ÁÕº7,’˝∑Ω–ŒPQMN”ΰ˜ABC÷ÿµ˛≤ø∑÷Õº–Œ «’˝∑Ω–ŒMNPQ,
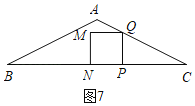
S£ΩPQ2£Ω£®2©Åt£©2£Ωt2©Å4t+4;
◊€…œ,S”Ît÷ƺ‰µƒ∫Ø ˝πÿœµ ΩŒ™:S£Ω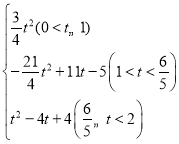 £ª
£ª
£®4£©¥Ê‘⁄Àƒ÷÷«Èøˆ:
¢Ÿ»ÁÕº8,M‘⁄÷–ŒªœþMQ…œ,‘ÚQ «ABµƒ÷–µ„,BQ£Ω![]() ,
,
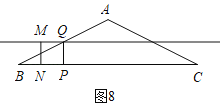
°ýBP£Ω1£Ω2t,
t£Ω![]() ;
;
¢⁄»ÁÕº9,M‘⁄÷–ŒªœþMT…œ,‘ÚT «BCµƒ÷–µ„,BT£Ω2,

°ýMT°ŒAC,
°ý°œC£Ω°œBTM,
°ýtan°œBTM£Ω![]() ,
,
°ýNT£ΩBP,
°þBP+TN©ÅBT£ΩPN,
°ý2t+2t©Å2£Ωt,t£Ω![]() ;
;
¢€»ÁÕº10,M‘⁄÷–ŒªœþMQ…œ,
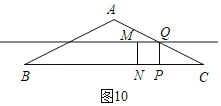
°ýQ «ACµƒ÷–µ„,
Õ¨¿Ìµ√CP£Ω1£Ω4©Å2t,t£Ω![]() ,
,
¢Ð»ÁÕº11,M‘⁄÷–ŒªœþMT…œ,T «BCµƒ÷–µ„,
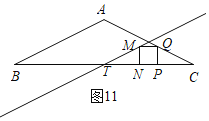
CP£ΩTN£Ω4©Å2t,PQ£ΩPN£Ω2©Åt,
°þCT£ΩTN+PN+PC,
°ý2£Ω2£®4©Å2t£©+2©Åt,
t£Ω![]() ;
;
◊€…œ,tµƒ÷µ «![]() √ΪÚ
√ΪÚ![]() √ΪÚ
√ΪÚ![]() √ΪÚ
√ΪÚ![]() √ΣÆ
√ΣÆ


 √˚ÂΩæÌœµ¡–¥∞∏
√˚ÂΩæÌœµ¡–¥∞∏ ”≈º”æ´æÌœµ¡–¥∞∏
”≈º”æ´æÌœµ¡–¥∞∏
| ƒÍº∂ | ∏þ÷–øŒ≥à | ƒÍº∂ | ≥ı÷–øŒ≥à |
| ∏þ“ª | ∏þ“ª√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı“ª | ≥ı“ª√‚∑—øŒ≥ÃÕ∆ºˆ£° |
| ∏þ∂˛ | ∏þ∂˛√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı∂˛ | ≥ı∂˛√‚∑—øŒ≥ÃÕ∆ºˆ£° |
| ∏þ»˝ | ∏þ»˝√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı»˝ | ≥ı»˝√‚∑—øŒ≥ÃÕ∆ºˆ£° |
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
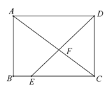
°æƒø°ø»ÁÕº£¨‘⁄æÿ–Œ ABCD ÷–£¨E «±þ BC ±þ…œ“ªµ„£¨¡¨Ω” DE Ωª∂‘Ω«œþ AC ”⁄µ„ F£¨»Ù AB=6£¨AD=8£¨BE=2£¨‘Ú AF µƒ≥§Œ™ _________________ ![]()
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø»ÁÕº1,‘⁄∆Ω√Ê÷±Ω«◊¯±Íœµ÷–,÷±œþ![]() ”Î≈◊ŒÔœþ
”Î≈◊ŒÔœþ![]() Ωª”⁄
Ωª”⁄![]() ¡Ωµ„£¨∆‰÷–
¡Ωµ„£¨∆‰÷–![]() ,
,![]() .∏√≈◊ŒÔœþ”Î
.∏√≈◊ŒÔœþ”Î![]() ÷·Ωª”⁄µ„
÷·Ωª”⁄µ„![]() ,”Î
,”Î![]() ÷·Ωª”⁄¡Ì“ªµ„
÷·Ωª”⁄¡Ì“ªµ„![]() .
.

(1)«Û![]() µƒ÷µº∞∏√≈◊ŒÔœþµƒΩ‚Œˆ Ω;
µƒ÷µº∞∏√≈◊ŒÔœþµƒΩ‚Œˆ Ω;
(2)»ÁÕº2.»Ùµ„![]() Œ™œþ∂Œ
Œ™œþ∂Œ![]() …œµƒ“ª∂ص„(≤ª”Î
…œµƒ“ª∂ص„(≤ª”Î![]() ÷ÿ∫œ).∑÷±“‘
÷ÿ∫œ).∑÷±“‘![]() °¢
°¢![]() Œ™–±±þ,‘⁄÷±œþ
Œ™–±±þ,‘⁄÷±œþ![]() µƒÕ¨≤ý◊˜µ»—¸÷±Ω«°˜
µƒÕ¨≤ý◊˜µ»—¸÷±Ω«°˜![]() ∫Õµ»—¸÷±Ω«°˜
∫Õµ»—¸÷±Ω«°˜![]() ,¡¨Ω”
,¡¨Ω”![]() , ‘»∑∂®°˜
, ‘»∑∂®°˜![]() √ʪ˝◊Ó¥Û ±
√ʪ˝◊Ó¥Û ±![]() µ„µƒ◊¯±Í.
µ„µƒ◊¯±Í.
(3)»ÁÕº3.¡¨Ω”![]() °¢
°¢![]() ,‘⁄œþ∂Œ
,‘⁄œþ∂Œ![]() …œ «∑ҥʑ⁄µ„
…œ «∑ҥʑ⁄µ„![]() , πµ√“‘
, πµ√“‘![]() Œ™∂•µ„µƒ»˝Ω«–Œ”ΰ˜
Œ™∂•µ„µƒ»˝Ω«–Œ”ΰ˜![]() œýÀ∆,»Ù¥Ê‘⁄,«Î÷±Ω”–¥≥ˆµ„
œýÀ∆,»Ù¥Ê‘⁄,«Î÷±Ω”–¥≥ˆµ„![]() µƒ◊¯±Í;»Ù≤ª¥Ê‘⁄,«ÎÀµ√˜¿Ì”….
µƒ◊¯±Í;»Ù≤ª¥Ê‘⁄,«ÎÀµ√˜¿Ì”….
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
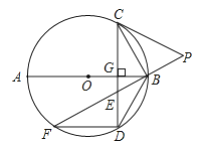
°æƒø°ø»ÁÕº£¨![]() Œ™
Œ™![]() µƒ÷±æ∂£¨
µƒ÷±æ∂£¨![]() ”⁄µ„
”⁄µ„![]() £¨
£¨![]() «
«![]() …œ“ªµ„£¨«“
…œ“ªµ„£¨«“![]() £¨—”≥§
£¨—”≥§![]() ÷¡µ„
÷¡µ„![]() £¨¡¨Ω”
£¨¡¨Ω”![]() £¨ π
£¨ π![]() £¨—”≥§
£¨—”≥§![]() ”Î
”Î![]() Ωª”⁄µ„
Ωª”⁄µ„![]() £¨¡¨Ω·
£¨¡¨Ω·![]() £¨
£¨![]() £Æ
£Æ
£®1£©¡¨Ω·![]() £¨«Û÷§£∫
£¨«Û÷§£∫![]() £ª
£ª
£®2£©«Û÷§£∫![]() «
«![]() µƒ«–œþ£ª
µƒ«–œþ£ª
£®3£©»Ù![]() £¨
£¨![]() £¨«Û
£¨«Û![]() µƒ÷µ£Æ
µƒ÷µ£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°øŒ Â÷≥ˆ
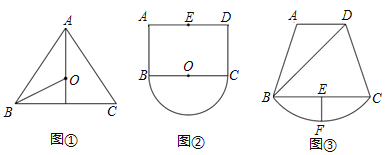
£®1£©»ÁÕº¢Ÿ£¨‘⁄°˜ABC÷–£¨AB£ΩAC£Ω10£¨BC£Ω12£¨µ„O «°˜ABCµƒÕ‚Ω”‘≤µƒ‘≤–ƒ£¨‘ÚOBµƒ≥§Œ™°° °°
Œ ÂÃΩæø
£®2£©»ÁÕº¢⁄£¨“—÷™æÿ–ŒABCD£¨AB£Ω4£¨AD£Ω6£¨µ„EŒ™ADµƒ÷–µ„£¨“‘BCŒ™÷±æ∂◊˜∞Α≤O£¨µ„PŒ™∞Α≤O…œ“ª∂ص„£¨«ÛE°¢P÷ƺ‰µƒ◊Ó¥Ûæý¿Î£ª
Œ Ã‚Ω‚æˆ
£®3£©ƒ≥µÿ”–“ªøÈ»ÁÕº¢€À˘ 浃π˚‘∞£¨π˚‘∞ «”…Àƒ±þ–ŒABCD∫Õœ“CB”Î∆‰À˘∂‘µƒ¡”ª°≥°µÿ◊È≥…µƒ£¨π˚‘∞÷˜»Àœ÷“™¥”»Îø⁄DµΩ![]() …œµƒ“ªµ„P–ÞΩ®“ªÃı± ÷±µƒ–°¬∑DP£Æ“—÷™AD°ŒBC£¨°œADB£Ω45°„£¨BD£Ω120
…œµƒ“ªµ„P–ÞΩ®“ªÃı± ÷±µƒ–°¬∑DP£Æ“—÷™AD°ŒBC£¨°œADB£Ω45°„£¨BD£Ω120![]() √◊£¨BC£Ω160√◊£¨π˝œ“BCµƒ÷–µ„E◊˜EF°ÕBCΩª
√◊£¨BC£Ω160√◊£¨π˝œ“BCµƒ÷–µ„E◊˜EF°ÕBCΩª![]() ”⁄µ„F£¨”÷≤‚µ√EF£Ω40√◊£Æ–ÞΩ®–°¬∑∆Ωæ˘√ø√◊–Ë“™40‘™£®–°¬∑øÌ∂»≤ªº∆£©£¨≤ªøº¬«∆‰À˚“ÚÀÿ£¨«Îƒ„∏˘æð“‘…œ–≈œ¢£¨∞Ô÷˙π˚‘∞÷˜»Àº∆À„–ÞΩ®’‚Ãı–°¬∑◊Ó∂ý“™ª®∑—∂ý…Ÿ‘™£ø
”⁄µ„F£¨”÷≤‚µ√EF£Ω40√◊£Æ–ÞΩ®–°¬∑∆Ωæ˘√ø√◊–Ë“™40‘™£®–°¬∑øÌ∂»≤ªº∆£©£¨≤ªøº¬«∆‰À˚“ÚÀÿ£¨«Îƒ„∏˘æð“‘…œ–≈œ¢£¨∞Ô÷˙π˚‘∞÷˜»Àº∆À„–ÞΩ®’‚Ãı–°¬∑◊Ó∂ý“™ª®∑—∂ý…Ÿ‘™£ø
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø»’’’º‰æýœµ ˝∑¥”≥¡À∑øŒð»’’’«Èøˆ£Æ»ÁÕº¢Ÿ£¨µ±«∞∫Û∑øŒð∂º≥؜ڒ˝ƒœ ±£¨»’’’º‰æýœµ ˝=L£∫£®H©ÅH1£©£¨∆‰÷–LŒ™¬•º‰ÀÆ∆Ωæý¿Î£¨HŒ™ƒœ≤ý¬•∑ø∏þ∂»£¨H1Œ™±±≤ý¬•∑øµ◊≤„¥∞î÷¡µÿ√Ê∏þ∂»£Æ
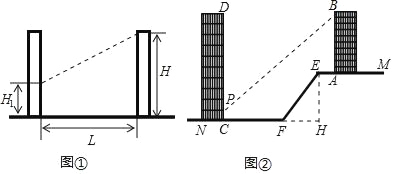
»ÁÕº¢⁄£¨…Ω∆¬EF≥ر±£¨EF≥§Œ™15m£¨∆¬∂»Œ™i=1£∫0.75£¨…Ω∆¬∂•≤ø∆ΩµÿEM…œ”–“ª∏þŒ™22.5mµƒ¬•∑øAB£¨µ◊≤øAµΩEµ„µƒæý¿ÎŒ™4m£Æ
£®1£©«Û…Ω∆¬EFµƒÀÆ∆ΩøÌ∂»FH£ª
£®2£©”˚‘⁄AB¬•’˝±±≤ý…ΩΩ≈µƒ∆ΩµÿFN…œΩ®“ª¬•∑øCD£¨“—÷™∏√¬•µ◊≤„¥∞îP¥¶÷¡µÿ√ÊC¥¶µƒ∏þ∂»Œ™0.9m£¨“™ π∏√¬•µƒ»’’’º‰æýœµ ˝≤ªµÕ”⁄1.25£¨µ◊≤øCæýF¥¶÷¡…Ÿ∂ý‘∂£ø
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
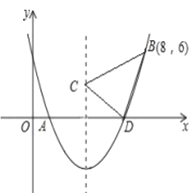
°æƒø°ø»ÁÕº£¨∂˛¥Œ∫Ø ˝![]() µƒÕºœÛΩª
µƒÕºœÛΩª![]() ÷·”⁄
÷·”⁄![]() ¡Ωµ„£¨≤¢æ≠π˝
¡Ωµ„£¨≤¢æ≠π˝![]() µ„£¨“—÷™
µ„£¨“—÷™![]() µ„◊¯±Í «
µ„◊¯±Í «![]() £¨
£¨![]() µ„◊¯±Í «
µ„◊¯±Í «![]() £Æ
£Æ
£®1£©«Û∂˛¥Œ∫Ø ˝µƒΩ‚Œˆ Ω£ª
£®2£©«Û∫Ø ˝ÕºœÛµƒ∂•µ„◊¯±Íº∞![]() µ„µƒ◊¯±Í£ª
µ„µƒ◊¯±Í£ª
£®3£©∂˛¥Œ∫Ø ˝µƒ∂‘≥∆÷·…œ «∑ҥʑ⁄“ªµ„![]() £¨ πµ√
£¨ πµ√![]() µƒ÷Ð≥§◊Ó–°£ø»Ù
µƒ÷Ð≥§◊Ó–°£ø»Ù![]() µ„¥Ê‘⁄£¨«Û≥ˆ
µ„¥Ê‘⁄£¨«Û≥ˆ![]() µ„µƒ◊¯±Í£¨»Ù
µ„µƒ◊¯±Í£¨»Ù![]() µ„≤ª¥Ê‘⁄£¨«ÎÀµ√˜¿Ì”…£Æ
µ„≤ª¥Ê‘⁄£¨«ÎÀµ√˜¿Ì”…£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°øƒ≥π´Àæº∆ªÆπ∫¬Ú2îª˙∆˜£¨∏√÷÷ª˙∆˜ π”√»˝ƒÍ∫Ûº¥±ªÃ‘Ã≠£Æª˙∆˜”–“ª“◊À¡„º˛£¨‘⁄π∫Ω¯ª˙∆˜ ±£¨ø…“‘∂ÓÕ‚π∫¬Ú’‚÷÷¡„º˛◊˜Œ™±∏º˛£¨√ø∏ˆ200‘™£Æ‘⁄ª˙∆˜ π”√∆⁄º‰£¨»Áπ˚±∏º˛≤ª◊„‘Ÿπ∫¬Ú£¨‘Ú√ø∏ˆ500‘™£¨»˝ƒÍ∫Û»Áπ˚±∏º˛∂ý”ý£¨√ø∏ˆ“‘![]() ‘™£®
‘™£®![]() £©ªÿ ’£Æœ÷–Ëæˆ≤þ‘⁄π∫¬Úª˙∆˜ ±”¶Õ¨ ±π∫¬Úº∏∏ˆ“◊À¡„º˛£¨Œ™¥ÀÀ—ºØ≤¢’˚¿Ì¡À100î’‚÷÷ª˙∆˜‘⁄»˝ƒÍ π”√∆⁄ƒ⁄∏¸ªªµƒ“◊À¡„º˛ ˝£¨µ√µΩ»Áœ¬∆µ ˝∑÷≤º÷±∑ΩÕº£∫
£©ªÿ ’£Æœ÷–Ëæˆ≤þ‘⁄π∫¬Úª˙∆˜ ±”¶Õ¨ ±π∫¬Úº∏∏ˆ“◊À¡„º˛£¨Œ™¥ÀÀ—ºØ≤¢’˚¿Ì¡À100î’‚÷÷ª˙∆˜‘⁄»˝ƒÍ π”√∆⁄ƒ⁄∏¸ªªµƒ“◊À¡„º˛ ˝£¨µ√µΩ»Áœ¬∆µ ˝∑÷≤º÷±∑ΩÕº£∫
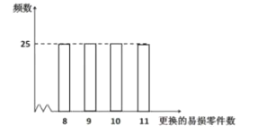
º«![]() ±Ì æ2îª˙∆˜»˝ƒÍƒ⁄π≤–Ë∏¸ªªµƒ“◊À¡„º˛ ˝£¨
±Ì æ2îª˙∆˜»˝ƒÍƒ⁄π≤–Ë∏¸ªªµƒ“◊À¡„º˛ ˝£¨![]() ±Ì æπ∫¬Ú2îª˙∆˜µƒÕ¨ ±π∫¬Úµƒ“◊À¡„º˛ ˝£Æ
±Ì æπ∫¬Ú2îª˙∆˜µƒÕ¨ ±π∫¬Úµƒ“◊À¡„º˛ ˝£Æ
£®1£©“‘100îª˙∆˜Œ™—˘±æ£¨«Î¿˚”√ª≠ ˜◊¥ÕºªÚ¡–±Ìµƒ∑Ω∑®π¿º∆![]() ≤ª≥¨π˝19µƒ∏≈¬ £ª
≤ª≥¨π˝19µƒ∏≈¬ £ª
£®2£©“‘’‚100îª˙∆˜‘⁄π∫¬Ú“◊À¡„º˛…œÀ˘–Ë∑—”√µƒ∆Ωæ˘ ˝Œ™æˆ≤þ“¿æ𣨑⁄![]() ”Î
”Î![]() ÷Æ÷–—°∆‰“ª£¨µ±
÷Æ÷–—°∆‰“ª£¨µ±![]() Œ™∫Œ÷µ ±£¨—°
Œ™∫Œ÷µ ±£¨—°![]() ±»ΩœªÆÀ„£ø
±»ΩœªÆÀ„£ø
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø»ÁÕº£¨’˝∑Ω–ŒOABCµƒ“ª∏ˆ∂•µ„O «∆Ω√Ê÷±Ω«◊¯±Íœµµƒ‘≠µ„£¨∂•µ„A£¨C∑÷±‘⁄y÷·∫Õx÷·…œ£¨PŒ™±þOC…œµƒ“ª∏ˆ∂ص„£¨«“PQ°ÕBP£¨PQ=BP£¨µ±µ„P¥”µ„C‘À∂ØµΩµ„O ±£¨ø…÷™µ„Q º÷’‘⁄ƒ≥∫Ø ˝ÕºœÛ…œ‘À∂Ø£¨‘Ú∆‰∫Ø ˝ÕºœÛ «£® £©
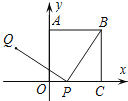
A.œþ∂ŒB.‘≤ª°
C.À´«˙œþµƒ“ª≤ø∑÷D.≈◊ŒÔœþµƒ“ª≤ø∑÷
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
π˙º —ß–£”≈—° - ¡∑œ∞≤·¡–±Ì - ‘¡–±Ì
∫˛±± °ª•¡™Õ¯Œ•∑®∫Õ≤ª¡º–≈œ¢æŸ±®∆Ωî | Õ¯…œ”–∫¶–≈œ¢æŸ±®◊®«¯ | µÁ–≈’©∆≠柱®◊®«¯ | …Ê¿˙ ∑–ÈŒÞ÷˜“”–∫¶–≈œ¢æŸ±®◊®«¯ | …Ê∆Û«÷»®æŸ±®◊®«¯
Œ•∑®∫Õ≤ª¡º–≈œ¢æŸ±®µÁª∞£∫027-86699610 柱®” œ‰£∫58377363@163.com