
【题目】如图,![]() 为
为![]() 的直径,
的直径,![]() 于点
于点![]() ,
,![]() 是
是![]() 上一点,且
上一点,且![]() ,延长
,延长![]() 至点
至点![]() ,连接
,连接![]() ,使
,使![]() ,延长
,延长![]() 与
与![]() 交于点
交于点![]() ,连结
,连结![]() ,
,![]() .
.
(1)连结![]() ,求证:
,求证:![]() ;
;
(2)求证:![]() 是
是![]() 的切线;
的切线;
(3)若![]() ,
,![]() ,求
,求![]() 的值.
的值.
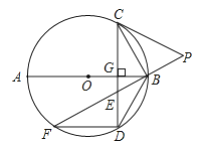
【答案】(1)见解析;(2)见解析;(3)![]()
【解析】
(1)根据等边对等角可得∠CDB=∠FBD,然后根据同弧所对的圆周角相等可得∠BCD=∠F,最后利用AAS即可证出结论;
(2)连接OC,根据圆周角定理和三角形外角的性质证出∠COB=∠CEB,然后根据等边对等角、直角三角形的性质和等量代换即可求出∠OCP=90°,最后根据切线的判定定理即可证出结论;
(3)连接AC,先证出∠F=∠A=∠BCG,根据等角的正切值相等可得![]() ,设CG=2x,则AG=3x,BG=
,设CG=2x,则AG=3x,BG=![]() ,然后根据题意列出方程即可求出CG、AG、BG、AB,然后根据垂径定理求出DG,最后根据tan∠COB = tan∠CEB,即可求出结论.
,然后根据题意列出方程即可求出CG、AG、BG、AB,然后根据垂径定理求出DG,最后根据tan∠COB = tan∠CEB,即可求出结论.
解:(1)∵![]()
∴∠CDB=∠FBD
∵![]()
∴∠BCD=∠F
在△BCD和△DFB中
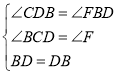
∴![]()
(2)连接OC
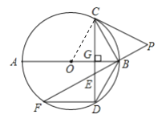
∵∠COB=2∠CDB,∠CEB=∠EDB+∠EBD=2∠EDB
∴∠COB=∠CEB
∵![]()
∴∠PCE=∠CEB
∴∠COB=∠PCE
∵![]()
∴∠OGC=90°
∴∠COB+∠OCG=90°
∴∠PCE+∠OCG=90°
∴∠OCP=90°
即OC⊥PC
∴![]() 是
是![]() 的切线;
的切线;
(3)连接AC
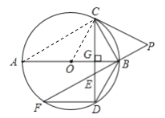
∴∠ACB=90°,
∴∠A+∠ACG=90°,∠BCG+∠ACG=90°
∴∠A=∠BCG
∵![]()
∴∠F=∠A=∠BCG
![]()
∴![]()
设CG=2x,则AG=3x,BG=![]()
∵![]()
∴![]()
∴CG=![]() ,AG=
,AG=![]() ,BG=
,BG=![]()
∴AB=AG+BG=![]() ,DG=CG=
,DG=CG=![]()
∴OB=![]() AB=
AB=![]()
∴OG=OB-BG=![]()
由(2)知∠COB=∠CEB
∴tan∠COB = tan∠CEB
∴![]()
即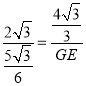
解得:GE=![]()
∴ED=DG-GE=![]()


科目:初中数学 来源: 题型:
【题目】某服装店同时购进甲、乙两种款式的运动服共![]() 套,进价和售价如表中所示,设购进甲款运动服
套,进价和售价如表中所示,设购进甲款运动服![]() 套(
套(![]() 为正整数),该服装店售完全部甲、乙两款运动服获得的总利润为
为正整数),该服装店售完全部甲、乙两款运动服获得的总利润为![]() 元.
元.
运动服款式 | 甲款 | 乙款 |
进价(元 |
|
|
售价(元 |
|
|
(1)求![]() 与
与![]() 的函数关系式;
的函数关系式;
(2)该服装店计划投入![]() 万元购进这两款运动服,则至少购进多少套甲款运动服?若售完全部的甲、乙两款运动服,则服装店可获得的最大利润是多少元?
万元购进这两款运动服,则至少购进多少套甲款运动服?若售完全部的甲、乙两款运动服,则服装店可获得的最大利润是多少元?
(3)在(2)的条件下,若服装店购进甲款运动服的进价降低![]() 元(其中
元(其中![]() ),且最多购进
),且最多购进![]() 套甲款运动服,若服装店保持这两款运动服的售价不变,请你设计出使该服装店获得最大销售利润的购进方案.
套甲款运动服,若服装店保持这两款运动服的售价不变,请你设计出使该服装店获得最大销售利润的购进方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在全国初中数学联赛中,将参赛两个班学生的成绩(得分均为整数)进行整理后分成五组,绘制出如下的频率分布直方图(如图所示),已知图中从左到右的第一、第三、第四、第五小组的频率分别是0.25、0.15、0.10、0.10,第二组的频数是40.
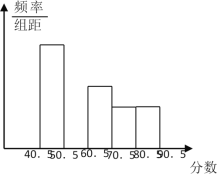
(1)第二小组的频率是_____,并补全这个频率分布直方图;
(2)这两个班参赛的学生人数是_________;
(3)这两个班参赛学生的成绩的中位数落在第______组内.(不必说明理由)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在![]() 中,
中,![]() ,
,![]() ,
,![]() 是
是![]() 上一点,连接
上一点,连接![]()
(1)如图1,若![]() ,
,![]() 是
是![]() 延长线上一点,
延长线上一点,![]() 与
与![]() 垂直,求证:
垂直,求证:![]()
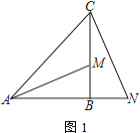
(2)过点![]() 作
作![]() ,
,![]() 为垂足,连接
为垂足,连接![]() 并延长交
并延长交![]() 于点
于点![]() .
.
①如图2,若![]() ,求证:
,求证:![]()
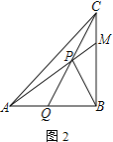
②如图3,若![]() 是
是![]() 的中点,直接写出
的中点,直接写出![]() 的值(用含
的值(用含![]() 的式子表示)
的式子表示)
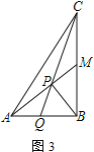
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形![]() 的边长为
的边长为![]() ,
,![]() 在正方形外,
在正方形外,![]() ,过
,过![]() 作
作![]() 于
于![]() ,直线
,直线![]() ,
,![]() 交于点
交于点![]() ,直线
,直线![]() 交直线
交直线![]() 于点
于点![]() ,则下列结论正确的是( )
,则下列结论正确的是( )

①![]() ;②
;②![]() ;③
;③![]() ;
;
④若![]() ,则
,则![]()
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】象棋是棋类益智游戏,中国象棋在中国有着三千多年的历史,由于用具简单,趣味性强,成为流行极为广泛的棋艺活动.李凯和张萌利用象棋棋盘和棋子做游戏.李凯将四枚棋子反面朝上放在棋盘上,其中有两个“兵”、一个“马”、一个“士”,张萌随机从这四枚棋子中摸一枚棋子,记下正汉字,然后再从剩下的三枚棋子中随机摸一枚.
(1)求张萌第一次摸到的棋子正面上的汉字是“兵”的概率;
(2)游戏规定:若张萌两次摸到的棋子中有“士”,则张萌胜;否则,李凯胜.请你用树状图或列表法求李凯胜的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,
,![]() .动点
.动点![]() 从点
从点![]() 出发,沿
出发,沿![]() 以每秒
以每秒![]() 个单位长度的速度向终点
个单位长度的速度向终点![]() 运动,当点
运动,当点![]() 与点
与点![]() 、
、![]() 不重合时,过点
不重合时,过点![]() 作
作![]() 交折线
交折线![]() 于点
于点![]() ,以
,以![]() 为边向左作正方形
为边向左作正方形![]() .设正方形
.设正方形![]() 与
与![]() 重叠部分图形的面积为
重叠部分图形的面积为![]() (平方单位),点
(平方单位),点![]() 运动的时间为
运动的时间为![]() (秒).
(秒).
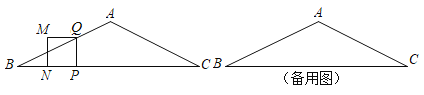
备用图
(1)用含![]() 的代数式表示
的代数式表示![]() 的长.
的长.
(2)直接写出点![]() 在
在![]() 内部时
内部时![]() 的取值范围.
的取值范围.
(3)求![]() 与
与![]() 之间的函数关系式.
之间的函数关系式.
(4)直接写出点![]() 落在
落在![]() 的中位线所在直线上时
的中位线所在直线上时![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
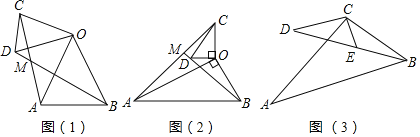
【题目】(操作发现)如图(1),在△OAB和△OCD中,OA=OB,OC=OD,∠AOB=∠COD=45°,连接AC,BD交于点M.
①AC与BD之间的数量关系为 ;
②∠AMB的度数为 ;
(类比探究)如图(2),在△OAB和△OCD中,∠AOB=∠COD=90°,∠OAB=∠OCD=30°,连接AC,交BD的延长线于点M.请计算![]() 的值及∠AMB的度数;
的值及∠AMB的度数;
(实际应用)如图(3),是一个由两个都含有30°角的大小不同的直角三角板ABC、DCE组成的图形,其中∠ACB=∠DCE=90°,∠A=∠D=30°且D、E、B在同一直线上,CE=1,BC=![]() ,求点A、D之间的距离.
,求点A、D之间的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AB是⊙O的直径,点D在⊙O上,∠DAB=45°,BC∥AD,CD∥AB.
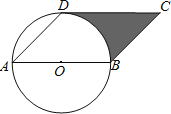
(1)判断直线CD与⊙O的位置关系,并说明理由;
(2)若⊙O的半径为1,求图中阴影部分的周长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com