
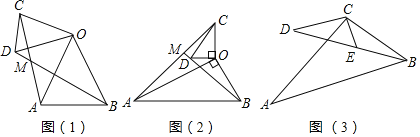
����Ŀ�����������֣���ͼ��1�����ڡ�OAB�͡�OCD�У�OA��OB��OC��OD����AOB����COD��45�㣬����AC��BD���ڵ�M��
��AC��BD֮���������ϵΪ�� ����
����AMB�Ķ���Ϊ�� ����
�����̽������ͼ��2�����ڡ�OAB�͡�OCD�У���AOB����COD��90�㣬��OAB����OCD��30�㣬����AC����BD���ӳ����ڵ�M�������![]() ��ֵ����AMB�Ķ�����
��ֵ����AMB�Ķ�����
��ʵ��Ӧ�ã���ͼ��3������һ��������������30��ǵĴ�С��ͬ��ֱ�����ǰ�ABC��DCE��ɵ�ͼ�Σ����С�ACB����DCE��90�㣬��A����D��30����D��E��B��ͬһֱ���ϣ�CE��1��BC��![]() �����A��D֮��ľ��룮
�����A��D֮��ľ��룮
���𰸡����������֡���AC=BD������AMB=45�㣻�����̽����![]() ����AMB=90�㣻��ʵ��Ӧ�á�4
����AMB=90�㣻��ʵ��Ӧ�á�4![]() ��5
��5![]()
��������
��������:��ͼ��1����֤����COA�ա�DOB��SAS�������ɽ�����⣮
���̽��:��ͼ��2����֤����COA�ס�ODB���ɵ�![]() ����MAK����OBK���ѽ���ɽ�����⣮
����MAK����OBK���ѽ���ɽ�����⣮
ʵ��Ӧ��:���������ν�ֱ�����������BE�����������������ε����ʽ�����⼴�ɣ�
�⣺��������:��ͼ��1���У���OA��BD��K��
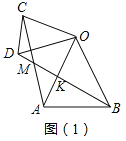
�ߡ�AOB����COD��45����
���COA����DOB��
��OA��OB��OC��OD��
���COA�ա�DOB��SAS����
��AC��DB����CAO����DBO��
�ߡ�MKA����BKO��
���AMK����BOK��45����
�ʴ�Ϊ��AC��BD����AMB��45��
���̽��:��ͼ��2���У�
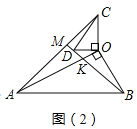
����OAB����OCD�У��ߡ�AOB����COD��90������OAB����OCD��30����
���COA����DOB��OC��![]() OD��OA��
OD��OA��![]() OB��
OB��
��![]() ��
��
���COA�ס�ODB��
��![]() ����MAK����OBK��
����MAK����OBK��
�ߡ�AKM����BKO��
���AMK����BOK��90����
ʵ��Ӧ��:��ͼ3��1�У���CH��BD��H������AD��
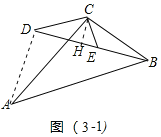
��Rt��DCE�У��ߡ�DCE��90������CDE��30����EC��1��
���CEH��60����
�ߡ�CHE��90����
���HCE��30����
��EH��![]() EC��
EC��![]() ��
��
��CH��![]() ��
��
��Rt��BCH��BH��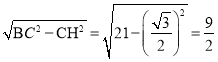 ��
��
��BE��BH��EH��4��
�ߡ�DCA�ס�ECB��
��AD��BE��CD��EC��![]() ��
��
��AD��4![]() ��
��
��ͼ3��2�У�����AD���� CH��DE��H��
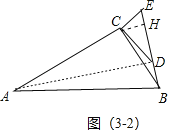
ͬ���ɵ�BH��![]() ��EH��
��EH��![]() ��
��
��BE��![]() +
+![]() ��5��
��5��
�ߡ�DCA�ס�ECB��
��AD��BE��CD��EC��![]() ��
��
��AD��5![]() ��
��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�̳�ͬʱ�����ס���������Ʒ��100��������ۺ��ۼ����±���
��Ʒ���� | �� | �� |
����(Ԫ/��) | 40 | 90 |
�ۼ�(Ԫ/��) | 60 | 120 |
�����м�����Ʒ����x�����̳�������100����Ʒ��������ΪyԪ��
(��)д��y����x�ĺ�����ϵʽ��
(��)���̳��ƻ����Ͷ��8000Ԫ���ڹ�����������Ʒ��
������Ҫ�������ټ�����Ʒ��
������������Щ��Ʒ�����̳��ɻ�õ���������Ƕ���Ԫ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
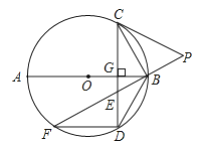
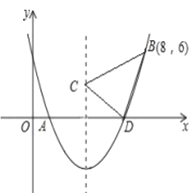
����Ŀ����ͼ��![]() Ϊ
Ϊ![]() ��ֱ����
��ֱ����![]() �ڵ�
�ڵ�![]() ��
��![]() ��
��![]() ��һ�㣬��
��һ�㣬��![]() ���ӳ�
���ӳ�![]() ����
����![]() ������
������![]() ��ʹ
��ʹ![]() ���ӳ�
���ӳ�![]() ��
��![]() ���ڵ�
���ڵ�![]() ������
������![]() ��
��![]() ��
��
��1������![]() ����֤��
����֤��![]() ��
��
��2����֤��![]() ��
��![]() �����ߣ�
�����ߣ�
��3����![]() ��
��![]() ����
����![]() ��ֵ��
��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����ռ��ϵ����ӳ�˷��������������ͼ������ǰ���ݶ���������ʱ�����ռ��ϵ��=L����H��H1��������LΪ¥��ˮƽ���룬HΪ�ϲ�¥���߶ȣ�H1Ϊ����¥���ײ㴰̨������߶ȣ�
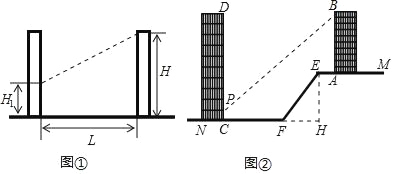
��ͼ�ڣ�ɽ��EF������EF��Ϊ15m���¶�Ϊi=1��0.75��ɽ�¶���ƽ��EM����һ��Ϊ22.5m��¥��AB���ײ�A��E��ľ���Ϊ4m��
��1����ɽ��EF��ˮƽ����FH��
��2������AB¥������ɽ�ŵ�ƽ��FN�Ͻ�һ¥��CD����֪��¥�ײ㴰̨P��������C���ĸ߶�Ϊ0.9m��Ҫʹ��¥�����ռ��ϵ��������1.25���ײ�C��F�����ٶ�Զ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�����κ���![]() ��ͼ��
��ͼ��![]() ����
����![]() ���㣬������
���㣬������![]() �㣬��֪
�㣬��֪![]() ��������
��������![]() ��
��![]() ��������
��������![]() ��
��
��1������κ����Ľ���ʽ��
��2������ͼ��Ķ������꼰![]() ������ꣻ
������ꣻ
��3�����κ����ĶԳ������Ƿ����һ��![]() ��ʹ��
��ʹ��![]() ���ܳ���С����
���ܳ���С����![]() ����ڣ����
����ڣ����![]() ������꣬��
������꣬��![]() �㲻���ڣ���˵�����ɣ�
�㲻���ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����2019�������γ������ɡ������¹������A����ȫ�������ɡ���B������������ɡ���C�������㽡���ܡ���С����С�ղ����˸������µ�־Ը�߷���������ί�������־Ը�߷��䵽������Ŀ�飮
��1��С�������䵽�����㽡���ܡ���Ŀ��ĸ���Ϊ�� ����
��2����С����С�ձ����䵽��ͬ��Ŀ��ĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��˾�ƻ�����2̨���������ֻ���ʹ���������̭��������һ����������ڹ�������ʱ�����Զ�������������Ϊ������ÿ��200Ԫ���ڻ���ʹ���ڼ䣬������������ٹ�����ÿ��500Ԫ�����������������࣬ÿ����![]() Ԫ��
Ԫ��![]() �����գ���������ڹ������ʱӦͬʱ�������������Ϊ���Ѽ���������100̨���ֻ���������ʹ�����ڸ�����������������õ�����Ƶ���ֲ�ֱ��ͼ��
�����գ���������ڹ������ʱӦͬʱ�������������Ϊ���Ѽ���������100̨���ֻ���������ʹ�����ڸ�����������������õ�����Ƶ���ֲ�ֱ��ͼ��
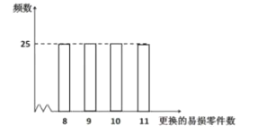
��![]() ��ʾ2̨���������ڹ�������������������
��ʾ2̨���������ڹ�������������������![]() ��ʾ����2̨������ͬʱ����������������
��ʾ����2̨������ͬʱ����������������
��1����100̨����Ϊ�����������û���״ͼ���б��ķ�������![]() ������19�ĸ��ʣ�
������19�ĸ��ʣ�
��2������100̨�����ڹ������������������õ�ƽ����Ϊ�������ݣ���![]() ��
��![]() ֮��ѡ��һ����
֮��ѡ��һ����![]() Ϊ��ֵʱ��ѡ
Ϊ��ֵʱ��ѡ![]() �Ƚϻ��㣿
�Ƚϻ��㣿
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����һ�������ĺ�����װ��4������1��2��3��4��С��������״����С��ȫ��ͬ��С���Ӻ��������ȡ��һ��С�������ϵ����֣���Ϊ��P�ĺ�����x���Ż�Ȼ�������ȡ��һ��С�������ϵ����֣���Ϊ��P��������y��
��1������״ͼ���б���д����P���п��ܵ����ꣻ
��2�������P����ԭ��ΪԲ�ģ�5Ϊ�뾶��Բ�ϵĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������֪����ͼ�٣�������![]() �У���
����![]() ��
��![]() ���ϣ�
���ϣ�![]() ƽ��
ƽ��![]() �������Ƿֱ��ӳ�
�������Ƿֱ��ӳ�![]() ��
��![]() �����ڵ�
�����ڵ�![]() ������֤
������֤![]() ��������Ҫ֤����
��������Ҫ֤����
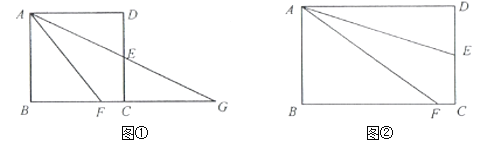
��̽������ͼ�ڣ��ھ���![]() �У���
����![]() ��
��![]() �ߵ��е㣬��
�ߵ��е㣬��![]() ��
��![]() ���ϣ�
���ϣ�![]() ƽ��
ƽ��![]() ����֤��
����֤��![]() ��
��
��Ӧ�ã��ڣ�̽�����������£���![]() ��
��![]() ��ֱ��д��
��ֱ��д��![]() �ij���
�ij���
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com