
����Ŀ����ͼ1,��ƽ��ֱ������ϵ��,ֱ��![]() ��������
��������![]() ����
����![]() ���㣬����
���㣬����![]() ,
,![]() .����������
.����������![]() �ύ�ڵ�
�ύ�ڵ�![]() ,��
,��![]() �ύ����һ��
�ύ����һ��![]() .
.

(1)��![]() ��ֵ���������ߵĽ���ʽ;
��ֵ���������ߵĽ���ʽ;
(2)��ͼ2.����![]() Ϊ�߶�
Ϊ�߶�![]() �ϵ�һ����(����
�ϵ�һ����(����![]() �غ�).�ֱ���
�غ�).�ֱ���![]() ��
��![]() Ϊб��,��ֱ��
Ϊб��,��ֱ��![]() ��ͬ��������ֱ����
��ͬ��������ֱ����![]() �͵���ֱ����
�͵���ֱ����![]() ,����
,����![]() ,��ȷ����
,��ȷ����![]() ������ʱ
������ʱ![]() �������.
�������.
(3)��ͼ3.����![]() ��
��![]() ,���߶�
,���߶�![]() ���Ƿ���ڵ�
���Ƿ���ڵ�![]() ,ʹ����
,ʹ����![]() Ϊ���������������
Ϊ���������������![]() ����,������,��ֱ��д����
����,������,��ֱ��д����![]() ������;��������,��˵������.
������;��������,��˵������.
���𰸡���1��![]() ����2����
����2����![]() ����
����![]() ʱ��
ʱ��![]() ���ʱ
���ʱ![]() ,����
,����![]() ����3�����ڵ�
����3�����ڵ�![]() ����Ϊ
����Ϊ![]() ��
��![]() .
.
����������1����A��B�������һ�κ�������ʽ���m��n��ֵ��ȷ����A��B������������κ�������ʽ���b��c��ֵ������
��2���ɵ���ֱ�ǡ�APM�͵���ֱ�ǡ�DPN���õ���MPNΪֱ��������ֱ�DZ߳˻���һ���ʾ��������MPN��������ö��κ�������ȷ����������������ʱP�����꼴����
��3��������������������������Ƶñ��������AQ�ij������������ľ��빫ʽ���Q���꼴�ɣ�
��1����A��m��0����B��4��n������y=x��1����m=1��n=3����A��1��0����B��4��3����
��y=��x2+bx+c������A���B����![]() �������
�������![]() ������κ�������ʽΪy=��x2+6x��5��
������κ�������ʽΪy=��x2+6x��5��
��2����ͼ2����APM���DPN��Ϊ����ֱ�������������APM=��DPN=45�㣬���MPN=90�㣬���MPNΪֱ�����������x2+6x��5=0���õ�x=1��x=5����D��5��0������DP=5��1=4����AP=m������DP=4��m����PM=![]() m��PN=
m��PN=![]() ��4��m������S��MPN=
��4��m������S��MPN=![]() PMPN=
PMPN=![]() ��
��![]() m��
m��![]() ��4��m��=��
��4��m��=��![]() m2��m=��
m2��m=��![]() ��m��2��2+1���൱m=2����AP=2ʱ��S��MPN�������ʱOP=3����P��3��0����
��m��2��2+1���൱m=2����AP=2ʱ��S��MPN�������ʱOP=3����P��3��0����
��3����������ֱ��CD����ʽΪy=x��5����Q��x��x��5���������������BAD=��ADC=45�㣬���������������
������ABD�ס�DAQʱ��![]() =
=![]() ����
����![]() =
=![]() �������AQ=
�������AQ=![]() ���������ľ��빫ʽ������x��1��2+��x��5��2=
���������ľ��빫ʽ������x��1��2+��x��5��2=![]() �������x=
�������x=![]() ����ʱQ��
����ʱQ��![]() ����
����![]() ����
����
�ڵ���ABD�ס�DQAʱ��![]() =1����AQ=
=1����AQ=![]() ������x��1��2+��x��5��2=10�������x=2����ʱQ��2����3����
������x��1��2+��x��5��2=10�������x=2����ʱQ��2����3����
��������Q��������2����3����![]() ����
����![]() ����
����


 ��У��������ĩ��̾�ϵ�д�
��У��������ĩ��̾�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵ�У���֪���κ���y=ax2��2ax��3a��a��0��ͼ����x�ύ�ڵ�A��B����A�ڵ�B����ࣩ����y�ύ�ڵ�C������ΪD��
��1�����A��B�����ꣻ
��2����MΪ�Գ�����x�ύ�㣬��DM=2AM��
������κ�������ʽ��
����t��2��x��tʱ�����κ��������ֵ5����tֵ��
����ֱ��x=4��������߽��ڵ�E������������C��E֮��IJ��ּ�Ϊͼ���Ϊͼ��P����C��E���㣩����ͼ��P��ֱ��x=4���ۣ��õ�ͼ��Q���ֹ��㣨10����4����ֱ��y=kx+b��ͼ��P��ͼ��Q���ཻ����ֻ���������㣬��b��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ÿ��С�����εı߳�Ϊ1�������У���A��B��Ϊ��㣮
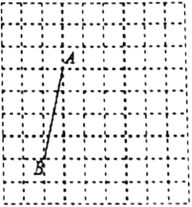
(��)AB�ij�����_____��
(��)����C����ABΪ�ױߵĵ���ֱ�������εĶ��㣬��D�ڱ�AC�ϣ�������S��ABD=![]() S��ABC��������ͼ��ʾ�������У����̶ȵ�ֱ�ߣ������߶�BD������Ҫ˵����D��λ��������ҵ���(��Ҫ��֤��)______��
S��ABC��������ͼ��ʾ�������У����̶ȵ�ֱ�ߣ������߶�BD������Ҫ˵����D��λ��������ҵ���(��Ҫ��֤��)______��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ȫ��������ѧ�����У�������������ѧ���ijɼ����÷־�Ϊ����������������ֳ����飬���Ƴ����µ�Ƶ�ʷֲ�ֱ��ͼ����ͼ��ʾ������֪ͼ�д����ҵĵ�һ�����������ġ�����С���Ƶ�ʷֱ���0��25��0��15��0��10��0��10���ڶ����Ƶ����40��
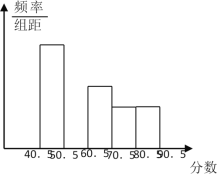
��1���ڶ�С���Ƶ����_____������ȫ���Ƶ�ʷֲ�ֱ��ͼ��
��2���������������ѧ��������_________��
��3�������������ѧ���ijɼ�����λ�����ڵ�______���ڣ�������˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
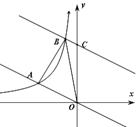
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�ֱ��![]() �뷴��������
�뷴��������![]()
![]() �ڵڶ������ڵ�ͼ���ཻ�ڵ�
�ڵڶ������ڵ�ͼ���ཻ�ڵ�![]() ����ֱ��
����ֱ��![]() ����ƽ�ƺ��뷴��������ͼ���ڵڶ������ڽ��ڵ�
����ƽ�ƺ��뷴��������ͼ���ڵڶ������ڽ��ڵ�![]() ����
����![]() �ύ�ڵ�
�ύ�ڵ�![]() ����
����![]() �����Ϊ3����ֱ��
�����Ϊ3����ֱ��![]() �Ĺ�ϵʽΪ��________
�Ĺ�ϵʽΪ��________
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����![]() �У�
��![]() ��
��![]() ��
��![]() ��
��![]() ��һ�㣬����
��һ�㣬����![]()
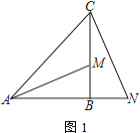
��1����ͼ1����![]() ��
��![]() ��
��![]() �ӳ�����һ�㣬
�ӳ�����һ�㣬![]() ��
��![]() ��ֱ����֤��
��ֱ����֤��![]()
��2������![]() ��
��![]() ��
��![]() Ϊ���㣬����
Ϊ���㣬����![]() ���ӳ���
���ӳ���![]() �ڵ�
�ڵ�![]() .
.
����ͼ2����![]() ����֤��
����֤��![]()
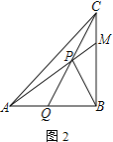
����ͼ3����![]() ��
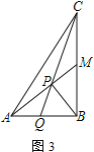
��![]() ���е㣬ֱ��д��
���е㣬ֱ��д��![]() ��ֵ���ú�
��ֵ���ú�![]() ��ʽ�ӱ�ʾ��
��ʽ�ӱ�ʾ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������![]() �ı߳�Ϊ
�ı߳�Ϊ![]() ��
��![]() ���������⣬
���������⣬![]() ����
����![]() ��
��![]() ��
��![]() ��ֱ��
��ֱ��![]() ��
��![]() ���ڵ�
���ڵ�![]() ��ֱ��
��ֱ��![]() ��ֱ��
��ֱ��![]() �ڵ�
�ڵ�![]() �������н�����ȷ���ǣ� ��
�������н�����ȷ���ǣ� ��

��![]() ����
����![]() ����
����![]() ��
��
����![]() ����
����![]()
A.1��B.2��C.3��D.4��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����![]() �У�
��![]() ��
��![]() ������
������![]() �ӵ�
�ӵ�![]() ��������
��������![]() ��ÿ��
��ÿ��![]() ����λ���ȵ��ٶ����յ�
����λ���ȵ��ٶ����յ�![]() �˶�������
�˶�������![]() ���
���![]() ��
��![]() ���غ�ʱ������
���غ�ʱ������![]() ��
��![]() ������
������![]() �ڵ�
�ڵ�![]() ����
����![]() ��������������
��������������![]() ����������
����������![]() ��
��![]() �ص�����ͼ�ε����Ϊ
�ص�����ͼ�ε����Ϊ![]() ��ƽ����λ������
��ƽ����λ������![]() �˶���ʱ��Ϊ
�˶���ʱ��Ϊ![]() ���룩��
���룩��
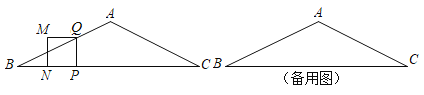
�������� ����ͼ
��1���ú�![]() �Ĵ���ʽ��ʾ
�Ĵ���ʽ��ʾ![]() �ij���
�ij���
��2��ֱ��д����![]() ��
��![]() �ڲ�ʱ
�ڲ�ʱ![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
��3����![]() ��
��![]() ֮��ĺ�����ϵʽ��
֮��ĺ�����ϵʽ��
��4��ֱ��д����![]() ����
����![]() ����λ������ֱ����ʱ
����λ������ֱ����ʱ![]() ��ֵ��
��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��һ�����ǰ壨��ABC����DEF����ͼ���ã���D��AB���ϻ�����DE��AC�ڵ�G��DF��BC�ڵ�H�����ڻ���������ʼ�ձ���DG��DH����AC��2������BDH��������ֵ�ǣ� ��
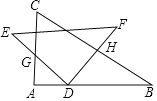
A.3B.3![]() C.
C.![]() D.
D.![]()
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com