
ЁОЬтФПЁПФГГЌЪаМЦЛЎЙКНјвЛХњМзЁЂввСНжжЭцОпЃЌвбжЊ4МўМзжжЭцОпЕФНјМлгы2МўввжжЭцОпЕФНјМлЕФКЭЮЊ230дЊЃЌ2МўМзжжЭцОпЕФНјМлгы3МўввжжЭцОпЕФНјМлЕФКЭЮЊ185дЊЃЎ
ЃЈ1ЃЉЧѓУПМўМзжжЁЂввжжЭцОпЕФНјМлЗжБ№ЪЧЖрЩйдЊЃЛ
ЃЈ2ЃЉШчЙћЙКНјМзжжЭцОпгагХЛнЃЌгХЛнЗНЗЈЪЧЃКЙКНјМзжжЭцОпГЌЙ§20МўЃЌГЌГіВПЗжПЩвдЯэЪм7елгХЛнЃЌШєЙКНј![]() ЃЈ
ЃЈ![]() ЃЉМўМзжжЭцОпашвЊЛЈЗб
ЃЉМўМзжжЭцОпашвЊЛЈЗб![]() дЊЃЌЧыФужБНгаДГі
дЊЃЌЧыФужБНгаДГі![]() гы
гы![]() ЕФКЏЪ§БэДяЪНЃЎ
ЕФКЏЪ§БэДяЪНЃЎ
ЁОД№АИЁПЃЈ1ЃЉУПМўМзжжЭцОпЕФНјМлЪЧ40дЊЃЌУПМўввжжЭцОпЕФНјМлЪЧ35дЊЃЛЃЈ2ЃЉЕБ![]() ЪБЃЌ
ЪБЃЌ![]() ЃЛЕБ
ЃЛЕБ![]() ЪБЃЌ
ЪБЃЌ![]()
ЁОНтЮіЁП
ЃЈ1ЃЉЯШевГіЕШСПЙиЯЕЃК4МўМзжжЭцОпЕФНјМлгы2МўввжжЭцОпЕФНјМлЕФКЭЮЊ230дЊЃЌ2МўМзжжЭцОпЕФНјМлгы3МўввжжЭцОпЕФНјМлЕФКЭЮЊ185дЊЃЌдйСаГіЗНГЬзщЧѓНтМДЕУЃЎ
ЃЈ2ЃЉЯШНЋ![]() ЕФШЁжЕЗЖЮЇЗжСНЖЮЃК
ЕФШЁжЕЗЖЮЇЗжСНЖЮЃК![]() КЭ
КЭ![]() ЃЌдйИљОнЁАзмЗбгУ=Ъ§СП
ЃЌдйИљОнЁАзмЗбгУ=Ъ§СП![]() НјМлЁБСаГіЖдгІЗЖЮЇЕФКЏЪ§ЙиЯЕЪНЃЎ
НјМлЁБСаГіЖдгІЗЖЮЇЕФКЏЪ§ЙиЯЕЪНЃЎ
НтЃКЃЈ1ЃЉЩшУПМўМзжжЭцОпЕФНјМлЪЧ![]() дЊЃЌУПМўввжжЭцОпЕФНјМлЪЧ
дЊЃЌУПМўввжжЭцОпЕФНјМлЪЧ![]() дЊЃЎ
дЊЃЎ
гЩЬтвтЕУ![]()
НтЕУЃК![]()
Д№ЃКУПМўМзжжЭцОпЕФНјМлЪЧ40дЊЃЌУПМўввжжЭцОпЕФНјМлЪЧ35дЊЃЎ
ЃЈ2ЃЉЁпУПМўМзжжЭцОпЕФНјМлЪЧ40дЊ
ЁрЕБ![]() ЪБЃЌ
ЪБЃЌ![]() ЃЛ
ЃЛ
ЁпЙКНјМзжжЭцОпГЌЙ§20МўЃЌГЌГіВПЗжПЩвдЯэЪм7елгХЛн
ЁрЕБ![]() ЪБЃЌ
ЪБЃЌ![]() МД
МД![]()
злЩЯЫљЪіЃКЕБ![]() ЪБЃЌ
ЪБЃЌ![]() ЃЛЕБ
ЃЛЕБ![]() ЪБЃЌ
ЪБЃЌ![]()



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЫљЪОЪЧЖўДЮКЏЪ§yЃНax2+bx+cЃЈaЁй0ЃЉЭМЯѓЕФвЛВПЗжЃЌжБЯпxЃНЉ1ЪЧЖдГЦжсЃЌгаЯТСаХаЖЯЃКЂйbЉ2aЃН0ЃЌЂк4aЉ2b+cЃМ0ЃЌЂлaЉb+cЃНЉ9aЃЌЂмШєЃЈЉ3ЃЌy1ЃЉЃЌЃЈ![]() ЃЌy2ЃЉЪЧХзЮяЯпЩЯЕФСНЕуЃЌдђy1ЃМy2ЃЎЦфжае§ШЗЕФЪЧЃЈЁЁЁЁЃЉ
ЃЌy2ЃЉЪЧХзЮяЯпЩЯЕФСНЕуЃЌдђy1ЃМy2ЃЎЦфжае§ШЗЕФЪЧЃЈЁЁЁЁЃЉ
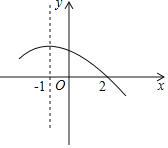
A. ЂйЂкЂлB. ЂйЂлC. ЂйЂмD. ЂйЂлЂм
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
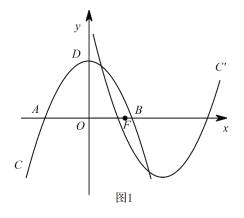
ЁОЬтФПЁПШчЭМ1ЃЌдкЦНУцжБНЧзјБъЯЕxOyжаЃЌХзЮяЯпCЃКy=ax2+bx+cгыxжсЯрНЛгкAЃЌBСНЕуЃЌЖЅЕуЮЊD(0ЃЌ4)ЃЌAB=4![]() ЃЌЩшЕуF(mЃЌ0)ЪЧxжсЕФе§АыжсЩЯвЛЕуЃЌНЋХзЮяЯпCШЦЕуFа§зЊ180ЁуЃЌЕУЕНаТЕФХзЮяЯпC/ЃЎ
ЃЌЩшЕуF(mЃЌ0)ЪЧxжсЕФе§АыжсЩЯвЛЕуЃЌНЋХзЮяЯпCШЦЕуFа§зЊ180ЁуЃЌЕУЕНаТЕФХзЮяЯпC/ЃЎ
(1)ЧѓХзЮяЯпCЕФКЏЪ§БэДяЪНЃЛ
(2)ШєХзЮяЯпC/гыХзЮяЯпCдкyжсЕФгвВргаСНИіВЛЭЌЕФЙЋЙВЕуЃЌЧѓmЕФШЁжЕЗЖЮЇЃЎ
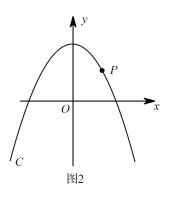
(3)ШчЭМ2ЃЌPЪЧЕквЛЯѓЯоФкХзЮяЯпCЩЯвЛЕуЃЌЫќЕНСНзјБъжсЕФОрРыЯрЕШЃЌЕуPдкХзЮяЯпC/ЩЯЕФЖдгІЕуP/ЃЌЩшMЪЧCЩЯЕФЖЏЕуЃЌNЪЧC/ЩЯЕФЖЏЕуЃЌЪдЬНОПЫФБпаЮPMP/NФмЗёГЩЮЊе§ЗНаЮЃПШєФмЃЌЧыжБНгаДГіmЕФжЕЃЛШєВЛФмЃЌЧыЫЕУїРэгЩЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌХзЮяЯпy=ax2+bx+cЃЈaЁй0ЃЉгыxжсНЛгкAЃЈЉ1ЃЌ0ЃЉЁЂBЃЈ3ЃЌ0ЃЉСНЕуЃЌгыyжсНЛгкЕуCЃЌЖЅЕуЮЊDЃЌЯТСаНсТле§ШЗЕФЪЧЃЈЁЁЁЁЃЉ
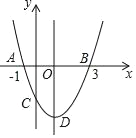
A. abcЃМ0
B. 3a+c=0
C. 4aЉ2b+cЃМ0
D. ЗНГЬax2+bx+c=Љ2ЃЈaЁй0ЃЉгаСНИіВЛЯрЕШЕФЪЕЪ§Иљ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
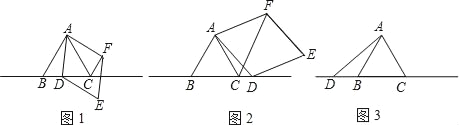
ЁОЬтФПЁПвбжЊЃЌЁїABCЮЊЕШБпШ§НЧаЮЃЌЕуDЮЊжБЯпBCЩЯвЛЖЏЕуЃЈЕуDВЛгыBЁЂCжиКЯЃЉЃЎвдADЮЊБпзїСтаЮADEFЃЌЪЙЁЯDAF=60ЁуЃЌСЌНгCFЃЎ
ЃЈ1ЃЉШчЭМ1ЃЌЕБЕуDдкБпBCЩЯЪБЃЌ
ЂйЧѓжЄЃКЁЯADB=ЁЯAFCЃЛЂкЧыжБНгХаЖЯНсТлЁЯAFC=ЁЯACB+ЁЯDACЪЧЗёГЩСЂЃЛ
ЃЈ2ЃЉШчЭМ2ЃЌЕБЕуDдкБпBCЕФбгГЄЯпЩЯЪБЃЌЦфЫћЬѕМўВЛБфЃЌНсТлЁЯAFC=ЁЯACB+ЁЯDACЪЧЗёГЩСЂЃПЧыаДГіЁЯAFCЁЂЁЯACBЁЂЁЯDACжЎМфДцдкЕФЪ§СПЙиЯЕЃЌВЂаДГіжЄУїЙ§ГЬЃЛ
ЃЈ3ЃЉШчЭМ3ЃЌЕБЕуDдкБпCBЕФбгГЄЯпЩЯЪБЃЌЧвЕуAЁЂFЗжБ№дкжБЯпBCЕФвьВрЃЌЦфЫћЬѕМўВЛБфЃЌЧыВЙШЋЭМаЮЃЌВЂжБНгаДГіЁЯAFCЁЂЁЯACBЁЂЁЯDACжЎМфДцдкЕФЕШСПЙиЯЕЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкЁбOжаЃЌABЪЧЁбOЕФжБОЖЃЌЕуDЪЧЁбOЩЯвЛЕуЃЌЕуCЪЧЛЁADЕФжаЕуЃЌЯвCEЁЭABгкЕуFЃЌЙ§ЕуDЕФЧаЯпНЛECЕФбгГЄЯпгкЕуGЃЌСЌНгADЃЌЗжБ№НЛCFЁЂBCгкЕуPЁЂQЃЌСЌНгACЃЎИјГіЯТСаНсТлЃКЂйЁЯBAD=ЁЯABCЃЛЂкGP=GDЃЛЂлЕуPЪЧЁїACQЕФЭтаФЃЛЂмAPAD=CQCBЃЎЦфжае§ШЗЕФЪЧЃЈЁЁЁЁЃЉ

A. ЂйЂкЂл B. ЂкЂлЂм C. ЂйЂлЂм D. ЂйЂкЂлЂм
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
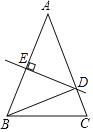
ЁОЬтФПЁПШчЭМЃЌдкЁїABCжаЃЌDEЪЧБпABЕФДЙжБЦНЗжЯпЃЌНЛABгкEЁЂНЛACгкDЃЌСЌНгBDЃЎ
ЃЈ1ЃЉШєABЃНACЃЌЧвЁїBCDЕФжмГЄЮЊ18cmЃЌЁїABCЕФжмГЄЮЊ30cmЃЌЧѓBEЕФГЄЃЛ
ЃЈ2ЃЉШєЁЯCBDЃН30ЁуЃЌЪдЧѓЁїABCШ§ИіНЧЕФЖШЪ§ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
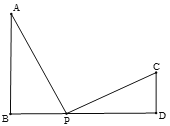
ЁОЬтФПЁПШчЭМЃЌвбжЊABЁЭBDЃЌCDЁЭBDЕуPЪЧBDЩЯвЛЕу.
ЃЈ1ЃЉШєЁЯAPC=90Ёу.ЧѓжЄЃКЁїPABЁзЁїCPDЃЛ
ЃЈ2ЃЉШєЁїPABгыЁїPCDЯрЫЦЃЌAB=9ЃЌBP=6ЃЌCD=4.ЧѓPDЕФГЄЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
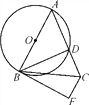
ЁОЬтФПЁПШчЭМЃЌдкЁїABCжаЃЌABЃНACЃЌвдABЮЊжБОЖЕФЁбOНЛACБпгкЕуDЃЌЙ§ЕуCзїCFЁЮABЃЌгыЙ§ЕуBЕФЧаЯпНЛгкЕуFЃЌСЌНгBD.
(1)ЧѓжЄЃКBDЃНBFЃЛ
(2)ШєABЃН10ЃЌCDЃН4ЃЌЧѓBCЕФГЄЃЎ
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com