
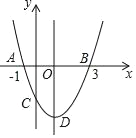
【题目】如图,抛物线y=ax2+bx+c(a≠0)与x轴交于A(﹣1,0)、B(3,0)两点,与y轴交于点C,顶点为D,下列结论正确的是( )
A. abc<0
B. 3a+c=0
C. 4a﹣2b+c<0
D. 方程ax2+bx+c=﹣2(a≠0)有两个不相等的实数根
【答案】B
【解析】
由图象可知a>0,b<0,c<0,即可判定选项A;由抛物线y=ax2+bx+c(a≠0)与x轴交于A(﹣1,0)、B(3,0)两点,可知抛物线的对称轴为x=1,即可得b=﹣2a,当x=﹣1时,y=a﹣b+c=a+2a+c=3a+c=0,由此即可判定选项B;当x=﹣2时,y=4a﹣2b+c>0,由此看判定选项C;由函数图象可知,如果函数y=ax2+bx+c(a≠0)顶点的纵坐标大于﹣2,则方程ax2+bx+c=﹣2(a≠0)没有实数根,由此可判定选项D.
由图象可得,a>0,b<0,c<0,
∴abc>0,故选项A错误,
∵抛物线y=ax2+bx+c(a≠0)与x轴交于A(﹣1,0)、B(3,0)两点,
∴﹣![]() =1,得b=﹣2a,
=1,得b=﹣2a,
当x=﹣1时,y=a﹣b+c=a+2a+c=3a+c=0,故选项B正确,
当x=﹣2时,y=4a﹣2b+c>0,故选项C错误,
由函数图象可知,如果函数y=ax2+bx+c(a≠0)顶点的纵坐标大于﹣2,则方程ax2+bx+c=﹣2(a≠0)没有实数根,故选项D错误,
故选B.


 品学双优卷系列答案
品学双优卷系列答案 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,AB=AD=6,AB⊥BC,AD⊥CD,∠BAD=60°,点M、N分别在AB、AD边上,若AM:MB=AN:ND=1:2,则tan∠MCN=

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两名同学进行射击训练,在相同条件下各射靶5次,成绩统计如下表:
命中环数 | 7 | 8 | 9 | 10 |
甲命中相应环数的次数 | 2 | 2 | 0 | 1 |
乙命中相应环数的次数 | 1 | 3 | 1 | 0 |
(1)求甲、乙两人射击成绩的平均数;
(2)甲、乙两人中,谁的射击成绩更稳定些?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列条件中,不能判断△ABC是直角三角形的是( )
A. a:b:c=3:4:5 B. ∠A:∠B:∠C=3:4:5
C. ∠A+∠B=∠C D. a:b:c=1:2:![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知:关于x的二次函数![]() 的图象与x轴交于点A(1,0)和点B,与y轴交于点C(0,3),抛物线的对称轴与x轴交于点D.
的图象与x轴交于点A(1,0)和点B,与y轴交于点C(0,3),抛物线的对称轴与x轴交于点D.
(1)求二次函数的表达式;
(2)在y轴上是否存在一点P,使△PBC为等腰三角形.若存在,请求出点P的坐标;
(3)有一个点M从点A出发,以每秒1个单位的速度在AB上向点B运动,另一个点N从点D与点M同时出发,以每秒2个单位的速度在抛物线的对称轴上运动,当点M到 达点B时,点M、N同时停止运动,问点M、N运动到何处时,△MNB面积最大,试求出最大面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某超市计划购进一批甲、乙两种玩具,已知4件甲种玩具的进价与2件乙种玩具的进价的和为230元,2件甲种玩具的进价与3件乙种玩具的进价的和为185元.
(1)求每件甲种、乙种玩具的进价分别是多少元;
(2)如果购进甲种玩具有优惠,优惠方法是:购进甲种玩具超过20件,超出部分可以享受7折优惠,若购进![]() (
(![]() )件甲种玩具需要花费
)件甲种玩具需要花费![]() 元,请你直接写出
元,请你直接写出![]() 与
与![]() 的函数表达式.
的函数表达式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,平面直角坐标系XOY中,若A(0,a)、B(b,0)且(a﹣4)2+![]() =0,以AB为直角边作等腰Rt△ABC,∠CAB=90°,AB=AC.
=0,以AB为直角边作等腰Rt△ABC,∠CAB=90°,AB=AC.
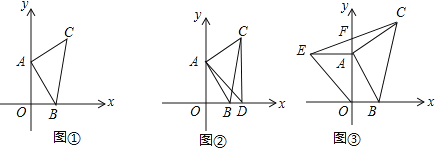
(1)求C点坐标;
(2)如图②过C点作CD⊥X轴于D,连接AD,求∠ADC的度数;
(3)如图③在(1)中,点A在Y轴上运动,以OA为直角边作等腰Rt△OAE,连接EC,交Y轴于F,试问A点在运动过程中S△AOB:S△AEF的值是否会发生变化?如果没有变化,请直接写出它们的比值 (不需要解答过程或说明理由).
查看答案和解析>>
科目:初中数学 来源: 题型:
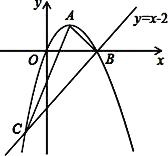
【题目】如图,已知抛物线经过原点O,顶点为A(1,1),且与直线y=x﹣2交于B,C两点.
⑴求抛物线的解析式及点C的坐标;
⑵求证:△ABC是直角三角形;
⑶若点N为x轴上的一个动点,过点N作MN⊥x轴与抛物线交于点M,则是否存在以O,M,N为顶点的三角形与△ABC相似?若存在,请求出点N的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com