
【题目】如图①,平面直角坐标系XOY中,若A(0,a)、B(b,0)且(a﹣4)2+![]() =0,以AB为直角边作等腰Rt△ABC,∠CAB=90°,AB=AC.
=0,以AB为直角边作等腰Rt△ABC,∠CAB=90°,AB=AC.
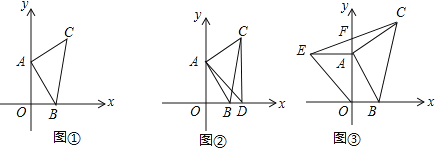
(1)求C点坐标;
(2)如图②过C点作CD⊥X轴于D,连接AD,求∠ADC的度数;
(3)如图③在(1)中,点A在Y轴上运动,以OA为直角边作等腰Rt△OAE,连接EC,交Y轴于F,试问A点在运动过程中S△AOB:S△AEF的值是否会发生变化?如果没有变化,请直接写出它们的比值 (不需要解答过程或说明理由).
【答案】(1)C点坐标为(4,5);(2)∠ADC=45°;(3)2.
【解析】试题分析:(1)作CM⊥OA于M,由非负性质求出a=4,b=1,由AAS证明△CAM≌△ABO,得出MC=OA=4,MA=OB=1,求出OM=OA+MA=5,即可得出C点坐标;
(2)证出OD=OA,得出△OAD为等腰直角三角形,得出∠ADO=45°,求出∠ADC=45°即可;
(3)先判断出△AEF≌△MCF,进而求出AM,最后用三角形的面积公式即可得出结论;
试题解析:(1)作CM⊥OA于M,如图①所示:
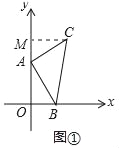
则∠CMA=∠AOB=90°,
∴∠OAB+∠ABO=90°,
∵(a﹣4)2+![]() =0,
=0,
∴a﹣4=0,b﹣1=0,
∴a=4,b=1,
∴OA=4,OB=1,
∵∠CAB=90°,
∴∠OAB+∠CAM=90°,
∴∠CAM=∠ABO,
在△CAM和△ABO中,
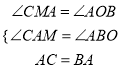 ,
,
∴△CAM≌△ABO(AAS),
∴MC=OA=4,MA=OB=1,
∴OM=OA+MA=5,
∴C点坐标为(4,5);
(2)∵CD⊥x轴,∴D(4,0),
∴OD=OA,
∴△OAD为等腰直角三角形,
∴∠ADO=45°,
∴∠ADC=90°﹣45°=45°;
(3)A点在运动过程中S△AOB:S△AEF的值不会发生变化,S△AOB:S△AEF=2;
理由如下:作CM⊥OA于M,如图③所示:
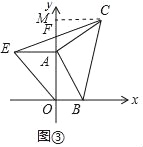
由(1)知,A(0,4),C(4,5),
∴OA=CM=4,
∵△AEO是等腰直角三角形,
∴AE=OA=4,∠OAE=90°,
∴∠EAF=∠OAE=90°=∠CMF,
∵∠AFE=∠MFC,AE=CM,
∴△AEF≌△MCF,
∴AF=MF=![]() AM,
AM,
∵C(4,5),A(0,4),
∴AM=1,
∴MF=![]() ,
,
∴S△AEF=S△MCF=![]() MF×CM=
MF×CM=![]() ×
×![]() ×4=1,
×4=1,
S△AOB=![]() OA×OB=
OA×OB=![]() ×4×1=2,
×4×1=2,
∴S△AOB:S△AEF=2:1=2,
即S△AOB:S△AEF的值是定值,不会发生变化.


 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案科目:初中数学 来源: 题型:
【题目】如图,已知直线l1∥l2,且l3和l1、l2分别交于A、B两点,点P在直线AB上.
(1)试说明∠1,∠2,∠3之间的关系式;(要求写出推理过程)
(2)如果点P在A、B两点之间(点P和A、B不重合)运动时,试探究∠1,∠2,∠3之间的关系是否发生变化?(只回答)
(3)如果点P在A、B两点外侧(点P和A、B不重合)运动时,试探究∠1,∠2,∠3之间的关系.(要求写出推理过程)
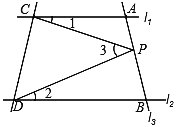
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:点A在射线CE上,∠C=∠D.
(1)如图1,若AC∥BD,求证:AD∥BC;
(2)如图2,若∠BAC=∠BAD,BD⊥BC,请探究∠DAE与∠C的数量关系,写出你的探究结论,并加以证明;
(3)如图3,在(2)的条件下,过点D作DF∥BC交射线于点F,当∠DFE=8∠DAE时,求∠BAD的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示是某一蓄水池每小时的排水量V(m3/h)与排完水池中的水所用的时间t(h)之间的函数关系图象.

①请你根据图象提供的信息求出此蓄水池的蓄水量;
②写出此函数的解析式;
③若要6h排完水池中的水,那么每小时的排水量应该是多少?
④如果每小时排水量是5m3,那么水池中的水将要多少小时排完?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某天,一蔬菜经营户用60元钱从蔬菜批发市场批了西红柿和豆角共40㎏到菜市场去卖,西红柿和豆角这天的批发价与零售价如下表所示:问:他当天卖完这些西红柿和豆角能赚多少钱?
品名 | 西红柿 | 豆角 |
批发价(单位:元/kg) | 1.2 | 1.6 |
零售价(单位:元/kg) | 1.8 | 2.5 |
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】两个大小不同的等腰直角三角形三角板如图1所示放置,图2是由它抽象出的几何图形,B,C,E在同一条直线上,连结DC.
(1)求证:△ABE≌△ACD;
(2)求证:DC⊥BE.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法中正确的是( ).
A. “打开电视机,正在播放《动物世界》”是必然事件
B. 某种彩票的中奖概率为![]() ,说明每买1000张,一定有一张中奖
,说明每买1000张,一定有一张中奖
C. 抛掷一枚质地均匀的硬币一次,出现正面朝上的概率为![]()
D. 想了解长沙市所有城镇居民的人均年收入水平,宜采用抽样调查
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com