
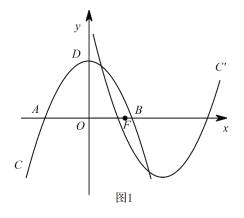
����Ŀ����ͼ1����ƽ��ֱ������ϵxOy�У�������C��y=ax2+bx+c��x���ཻ��A��B���㣬����ΪD(0��4)��AB=4![]() �����F(m��0)��x�����������һ�㣬��������C�Ƶ�F��ת180�����õ��µ�������C/��
�����F(m��0)��x�����������һ�㣬��������C�Ƶ�F��ת180�����õ��µ�������C/��
(1)��������C�ĺ�������ʽ��
(2)��������C/��������C��y����Ҳ���������ͬ�Ĺ����㣬��m��ȡֵ��Χ��
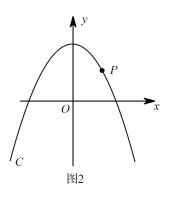
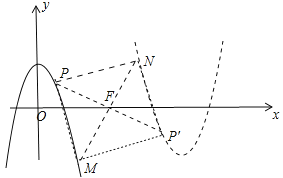
(3)��ͼ2��P�ǵ�һ������������C��һ�㣬������������ľ�����ȣ���P��������C/�ϵĶ�Ӧ��P/����M��C�ϵĶ��㣬N��C/�ϵĶ��㣬��̽���ı���PMP/N�ܷ��Ϊ�����Σ����ܣ���ֱ��д��m��ֵ�������ܣ���˵�����ɣ�
���𰸡���1��![]() ����2��2��m��
����2��2��m��![]() ����3��m=6��m=
����3��m=6��m=![]() ��3��
��3��
��������
���⣨1�������������ߵĶ���C��0��4����A��![]() ��0�����������ߵĽ���ʽΪ
��0�����������ߵĽ���ʽΪ![]() ����A��
����A��![]() ��0������ɵ�a=
��0������ɵ�a=![]() ���ɴ˼��ɽ�����⣻
���ɴ˼��ɽ�����⣻
��2��������������C���Ķ�������Ϊ��2m����4������������C���Ľ���ʽΪ![]() ����
����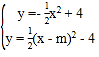 ����ȥy�õ�
����ȥy�õ�![]() �������⣬������C����������C��y����Ҳ���������ͬ�Ĺ����㣬����
�������⣬������C����������C��y����Ҳ���������ͬ�Ĺ����㣬����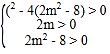 ���ⲻ��ʽ�鼴�ɽ�����⣻
���ⲻ��ʽ�鼴�ɽ�����⣻
��3������1���ı���PMP��N�ܳ�Ϊ�����Σ���PE��x����E��MH��x����H����������֪P��2��2��������PFM�ǵ���ֱ��������ʱ���ı���PMP��N�������Σ��Ƴ�PF=FM����PFM=90�㣬��֤��PFE�ա�FMH���ɵ�PE=FH=2��EF=HM=2��m���ɵ�M��m+2��m��2�������ɴ���ϵ�������ɽ�����⣻����2����ͼ���ı���PMP��N�������Σ�ͬ���ɵ�M��m��2��2��m�������ô���ϵ�������ɽ�����⣮
�����������1�������������ߵĶ���C��0��4����A��![]() ��0�����������ߵĽ���ʽΪ
��0�����������ߵĽ���ʽΪ![]() ����A��
����A��![]() ��0������ɵ�a=
��0������ɵ�a=![]() ����������C�ĺ�������ʽΪ
����������C�ĺ�������ʽΪ![]() ��
��
��2��������������C���Ķ�������Ϊ��2m����4������������C���Ľ���ʽΪ![]() ����
����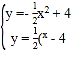 ����ȥy�õ�
����ȥy�õ�![]() �������⣬������C����������C��y����Ҳ���������ͬ�Ĺ����㣬����
�������⣬������C����������C��y����Ҳ���������ͬ�Ĺ����㣬����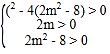 �����2��m��
�����2��m��![]() ��������������m��ȡֵ��ΧΪ2��m��
��������������m��ȡֵ��ΧΪ2��m��![]() ��
��
��3�����ۣ��ı���PMP��N�ܳ�Ϊ�����Σ�
���ɣ�1����1����ͼ����PE��x����E��MH��x����H��

��������֪P��2��2��������PFM�ǵ���ֱ��������ʱ���ı���PMP��N�������Σ���PF=FM����PFM=90�㣬��֤��PFE�ա�FMH���ɵ�PE=FH=2��EF=HM=2��m����M��m+2��m��2�����ߵ�M��![]() �ϣ���
�ϣ���![]() �����m=
�����m=![]() ��3��
��3��![]() ��3������������m=
��3������������m=![]() ��3ʱ���ı���PMP��N�������Σ�
��3ʱ���ı���PMP��N�������Σ�
����2����ͼ���ı���PMP��N�������Σ�ͬ���ɵ�M��m��2��2��m������M��m��2��2��m������![]() �У�
�У�![]() �����m=6��0������������m=6ʱ���ı���PMP��N�������Σ�
�����m=6��0������������m=6ʱ���ı���PMP��N�������Σ�
����������m=6��m=![]() ��3ʱ���ı���PMP��N�������Σ�
��3ʱ���ı���PMP��N�������Σ�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
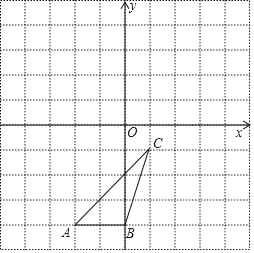
����Ŀ����ͼ����ABC�����������ֱ���A����2����4����B��0����4����C��1����1����
��1����ͼ�л�����ABC����ԭ��ԳƵġ�A1B1C1��
��2����ͼ�л�����ABC��ԭ��O��ʱ����ת90����ġ�A2B2C2��
��3���ڣ�2���������£����A�˶�·������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������֪���������ε�������������ƽ���ߵĽ��㣬�����������ĵ�һ��ֱ���������ཻ��������֮����߶ΰ���������ηֳ�����ͼ�Σ�����һ��ͼ����ԭ���������ƣ���������߶ν�����������εġ������ߡ���
��1���ȱ������Ρ������ߡ�������Ϊ�� ����
��2����ͼ����ABC�У�AB=AC����D��AC�ϣ���BD=BC=AD����֤��BD����ABC�ġ������ߡ���
��3����Rt��ABC�У���C=90�㣬AC=4��BC=3��E��F�ֱ��ڱ�AC��BC�ϣ���EF����ABC�ġ������ߡ�����EF�ij���

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ס�������ͬѧ�������ѵ��������ͬ�����¸����5�Σ��ɼ�ͳ�����±���
����� | 7 | 8 | 9 | 10 |
��������Ӧ�����Ĵ��� | 2 | 2 | 0 | 1 |
��������Ӧ�����Ĵ��� | 1 | 3 | 1 | 0 |
(1)��ס�����������ɼ���ƽ������
(2)�ס��������У�˭������ɼ����ȶ�Щ?��˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪������y=ax2+bx+3�ĶԳ�����ֱ��x=1��
��1����֤��2a+b=0��
��2��������x�ķ���ax2+bx��8=0��һ����Ϊ4���̵���һ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����![]() �У�
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ����
����![]() ��
��![]() �ϣ�
�ϣ�![]() ��
��![]() �ڵ�
�ڵ�![]() ��
��![]() ��
��![]() �ڵ�
�ڵ�![]() ����
����![]() ʱ��
ʱ��![]() ________��
________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
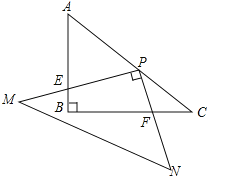
����Ŀ�����������У������жϡ�ABC��ֱ�������ε��ǣ�������
A. a��b��c��3��4��5 B. ��A����B����C��3��4��5
C. ��A+��B����C D. a��b��c��1��2��![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij���мƻ�����һ���ס���������ߣ���֪4��������ߵĽ�����2��������ߵĽ��۵ĺ�Ϊ230Ԫ��2��������ߵĽ�����3��������ߵĽ��۵ĺ�Ϊ185Ԫ��
��1����ÿ�����֡�������ߵĽ��۷ֱ��Ƕ���Ԫ��
��2�������������������Żݣ��Żݷ����ǣ�����������߳���20�����������ֿ�������7���Żݣ�������![]() ��
��![]() �������������Ҫ����
�������������Ҫ����![]() Ԫ������ֱ��д��
Ԫ������ֱ��д��![]() ��
��![]() �ĺ�������ʽ��
�ĺ�������ʽ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��һ�κ���![]() �ֱ�y�ᡢx����A��B���㣬������y=��x2+bx+c��A��B���㣮
�ֱ�y�ᡢx����A��B���㣬������y=��x2+bx+c��A��B���㣮
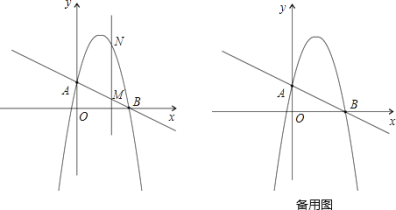
��1������������ߵĽ���ʽ��
��2������ֱx���ֱ��x=t���ڵ�һ����ֱ��AB��M���������������N����tȡ��ֵʱ��MN�����ֵ�����ֵ�Ƕ��٣�
��3���ڣ�2��������£���A��M��N��DΪ������ƽ���ı��Σ�����ĸ�����D�����꣮
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com