
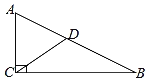
【题目】如图,在Rt△ABC中,∠ACB=90°,∠B=35°,CD是斜边AB上的中线,如果将△BCD沿CD所在直线翻折,点B落在点E处,联结AE,那么∠CAE的度数是_____度.
 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案科目:初中数学 来源: 题型:
【题目】“一方有难,八方支援”.四川汶川大地震牵动着全国人民的心,我市某医院准备从甲、乙、丙三位医生和A、B两名护士中选取一位医生和一名护士支援汶川.
(1)若随机选一位医生和一名护士,用树状图(或列表法)表示所有可能出现的结果;
(2)求恰好选中医生甲和护士A的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
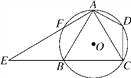
【题目】如图,已知四边形ABCD内接于⊙O,A是![]() 的中点,AE⊥AC于A,与⊙O及CB的延长线交于点F,E,且
的中点,AE⊥AC于A,与⊙O及CB的延长线交于点F,E,且![]() .
.
(1)求证:△ADC∽△EBA;
(2)如果AB=8,CD=5,求tan∠CAD的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
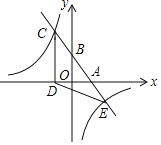
【题目】如图,一次函数y=kx+b(k、b为常数,k≠0)的图象与x轴、y轴分别交于A、B两点,且与反比例函数y=![]() (n为常数,且n≠0)的图象在第二象限交于点C.CD⊥x轴,垂足为D,若OB=2OA=3OD=12.
(n为常数,且n≠0)的图象在第二象限交于点C.CD⊥x轴,垂足为D,若OB=2OA=3OD=12.
(1)求一次函数与反比例函数的解析式;
(2)记两函数图象的另一个交点为E,求△CDE的面积;
(3)直接写出不等式kx+b≤![]() 的解集.
的解集.
查看答案和解析>>
科目:初中数学 来源: 题型:
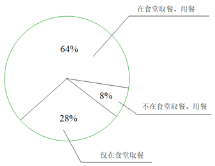
【题目】某公司有![]() 名职员,公司食堂供应午餐.受新冠肺炎疫情影响,公司停工了一段时间.为了做好复工后职员取餐、用餐的防疫工作,食堂进行了准备,主要如下:①将过去的自主选餐改为提供统一的套餐;②调查了全体职员复工后的午餐意向,结果如图
名职员,公司食堂供应午餐.受新冠肺炎疫情影响,公司停工了一段时间.为了做好复工后职员取餐、用餐的防疫工作,食堂进行了准备,主要如下:①将过去的自主选餐改为提供统一的套餐;②调查了全体职员复工后的午餐意向,结果如图![]() 所示;③设置不交叉的取餐区和用餐区,并将用餐区按一定的间距要求调整为可同时容纳
所示;③设置不交叉的取餐区和用餐区,并将用餐区按一定的间距要求调整为可同时容纳![]() 人用餐;④规定:排队取餐,要在食堂用餐的职员取餐后即进入用餐区用餐;⑤随机邀请了
人用餐;④规定:排队取餐,要在食堂用餐的职员取餐后即进入用餐区用餐;⑤随机邀请了![]() 名要在食堂取餐的职员进行了取餐、用餐的模拟演练,这
名要在食堂取餐的职员进行了取餐、用餐的模拟演练,这![]() 名职员取餐共用时
名职员取餐共用时![]() ,用餐时间(含用餐与回收餐具)如表所示.为节约时间,食堂决定将第一排用餐职员
,用餐时间(含用餐与回收餐具)如表所示.为节约时间,食堂决定将第一排用餐职员![]() 人的套餐先摆放在相应餐桌上,并在
人的套餐先摆放在相应餐桌上,并在![]() 开始用餐,其他职员则需自行取餐.
开始用餐,其他职员则需自行取餐.
用餐时间 | 人数 |
|
|
|
|
|
|
|
|
|
|
(1)食堂每天需要准备多少份午餐?
(2)食堂打算以参加演练的![]() 名职员用餐时间的平均数
名职员用餐时间的平均数![]() 为依据进行规划:前一批职员用餐
为依据进行规划:前一批职员用餐![]() 后,后一批在食堂用餐的职员开始取餐.为避免拥堵,需保证每位取餐后进入用餐区的职员都有座位用餐,则该规划是否可行?如果可行,请说明理由,并依此规划,根据调查统计的数据设计一个时间安排表,使得食堂不超过
后,后一批在食堂用餐的职员开始取餐.为避免拥堵,需保证每位取餐后进入用餐区的职员都有座位用餐,则该规划是否可行?如果可行,请说明理由,并依此规划,根据调查统计的数据设计一个时间安排表,使得食堂不超过![]() 就可结束取餐、用餐服务,开始消杀工作;如果不可行,也请说明理由.
就可结束取餐、用餐服务,开始消杀工作;如果不可行,也请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知半圆⊙O的直径AB=10,弦CD∥AB,且CD=8,E为弧CD的中点,点P在弦CD上,联结PE,过点E作PE的垂线交弦CD于点G,交射线OB于点F.
(1)当点F与点B重合时,求CP的长;
(2)设CP=x,OF=y,求y与x的函数关系式及定义域;
(3)如果GP=GF,求△EPF的面积.
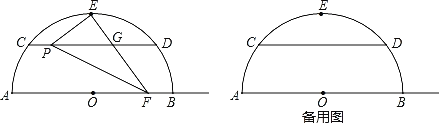
查看答案和解析>>
科目:初中数学 来源: 题型:
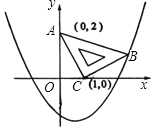
【题目】在平面直角坐标系中,现将一块等腰直角三角板放在第一象限,斜靠在两坐标轴上,且点A(0,2),点C(1,0),如图所示,抛物线y=ax2﹣ax﹣2经过点B.
(1)求点B的坐标;
(2)求抛物线的解析式;
(3)在抛物线上是否还存在点P(点B除外),使△ACP仍然是以AC为直角边的等腰直角三角形?若存在,求所有点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
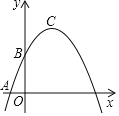
【题目】在平面直角坐标系xOy中(如图).已知抛物线y=﹣![]() x2+bx+c经过点A(﹣1,0)和点B(0,
x2+bx+c经过点A(﹣1,0)和点B(0,![]() ),顶点为C,点D在其对称轴上且位于点C下方,将线段DC绕点D按顺时针方向旋转90°,点C落在抛物线上的点P处.
),顶点为C,点D在其对称轴上且位于点C下方,将线段DC绕点D按顺时针方向旋转90°,点C落在抛物线上的点P处.
(1)求这条抛物线的表达式;
(2)求线段CD的长;
(3)将抛物线平移,使其顶点C移到原点O的位置,这时点P落在点E的位置,如果点M在y轴上,且以O、D、E、M为顶点的四边形面积为8,求点M的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AB=AC,以AC为直径的⊙O交BC于点![]() ,交AB于点E,点F为AC延长线上一点,且∠BAC=2∠CDF.
,交AB于点E,点F为AC延长线上一点,且∠BAC=2∠CDF.
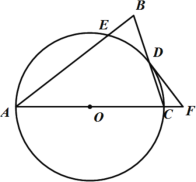
(1)求证:DF是⊙O的切线;
(2)连接DE,求证:DE=DB;
(3)若![]() ,CF=2,求⊙O的半径.
,CF=2,求⊙O的半径.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com