
【题目】如图,△ABC中,AB=AC,以AC为直径的⊙O交BC于点![]() ,交AB于点E,点F为AC延长线上一点,且∠BAC=2∠CDF.
,交AB于点E,点F为AC延长线上一点,且∠BAC=2∠CDF.
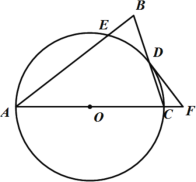
(1)求证:DF是⊙O的切线;
(2)连接DE,求证:DE=DB;
(3)若![]() ,CF=2,求⊙O的半径.
,CF=2,求⊙O的半径.
【答案】(1)见解析;(2)见解析;(3)7
【解析】
(1)连接AD,OD,根据等腰三角形性质证明∠CDF=∠ADO,证明∠ODF=90°则可得出结论;(2)由(1)得BD=DE=CD,即可证明;(3)证明△AFD∽△DFC,根据等比关系,可求出CD,DF长度,即可求出半径.
(1如图,
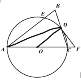
连接AD,OD,∵AC为直径,∴∠ADC=90°,
∴AD⊥CD,∵AB=AC,∴∠BAD=∠CAD=![]() ∠BAC,
∠BAC,
∵![]() ∠BAC=∠CDF,∴∠CDF=∠DAC,
∠BAC=∠CDF,∴∠CDF=∠DAC,
∵OA=OD,∴∠DAC=∠ADO,∴∠CDF=∠ADO,
∵∠ADO+∠ODC=90°,∴∠CDF+∠ODC=90°,
∴∠ODF=90°,∵OD为⊙O的半径,
∴DF是⊙O的切线.
(2)由(1)得,BD=CD,∠EAD=∠CAD,
∴BD=DE=CD,∴DE=DB.
(3)∵AB=AC,AD⊥BC,
∴BD=CD,
∵cosB=![]() ,∴AB=3BD,∴AC=3DC,
,∴AB=3BD,∴AC=3DC,
设CD=x,则AC=3x,∴AD=AC-CD,
∴AD=2![]() x,
x,
∵∠DAC=∠CDF,∠AFD=∠CFD,
∴△AFD∽△DFC,
∴![]() =
=![]() =
=![]() ,
,
∴![]() =
=![]() =
=![]() ,
,
∴DF=4![]() ,x=
,x=![]() ,
,
∴AC=3x=14,
∴⊙O的半径为7.


科目:初中数学 来源: 题型:
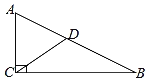
【题目】如图,在Rt△ABC中,∠ACB=90°,∠B=35°,CD是斜边AB上的中线,如果将△BCD沿CD所在直线翻折,点B落在点E处,联结AE,那么∠CAE的度数是_____度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△AOB中,∠AOB=90°,OA=3,OB=2,将Rt△AOB绕点O顺时针旋转90°后得Rt△FOE,将线段EF绕点E逆时针旋转90°后得线段ED,分别以O,E为圆心,OA、ED长为半径画弧AF和弧DF,连接AD,则图中阴影部分面积是( )
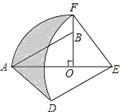
A. π B. ![]() C. 3+π D. 8﹣π
C. 3+π D. 8﹣π
查看答案和解析>>
科目:初中数学 来源: 题型:
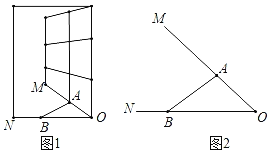
【题目】如图1,一扇窗户打开一定角度,其中一端固定在窗户边OM上的点A处,另一端B在边ON上滑动,图2为某一位置从上往下看的平面图,测得∠ABO为37°,∠AOB为45°,OB长为35厘米,求AB的长(参考数据:sin37°≈0.6,cos37°≈0.8,tan37°≈0.75)
查看答案和解析>>
科目:初中数学 来源: 题型:
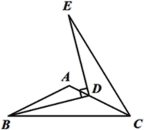
【题目】如图,在△ABC中,AB=AC=10,BC=![]() ,D为边AC上一动点(C点除外),把线段BD绕着点D沿着顺时针的方向旋转90°至DE,连接CE,则△CDE面积的最大值为______.
,D为边AC上一动点(C点除外),把线段BD绕着点D沿着顺时针的方向旋转90°至DE,连接CE,则△CDE面积的最大值为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某渔船在海面上朝正西方向以20海里/时匀速航行,在A处观测到灯塔C在北偏西60°方向上,航行1小时到达B处,此时观察到灯塔C在北偏西30°方向上,若该船继续向西航行至离灯塔距离最近的位置,求此时渔船到灯塔的距离(结果精确到1海里,参考数据: ![]() ≈1.732)
≈1.732)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】市实验中学计划在暑假第二周的星期一至星期五开展暑假社会实践活动,要求每位学生选择两天参加活动.
(1)甲同学随机选择连续的两天,其中有一天是星期三的概率是 ;
(2)乙同学随机选择两天,其中有一天是星期三的概率是多少?(列表或画树形图或列举)
查看答案和解析>>
科目:初中数学 来源: 题型:
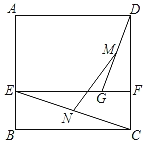
【题目】如图,已知正方形ABCD的边长为4,E,F分别为AB,CD边上的点,且EF∥BC,G为EF上一点,且GF=1,M,N分别为GD,EC的中点,则MN=_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠MON=30°,p是∠MON的角平分线,PQ平行ON交OM于点Q,以P为圆心半径为4的圆ON相切,如果以Q为圆心半径为r的圆与![]() 相交,那么r的取值范围是( )
相交,那么r的取值范围是( )
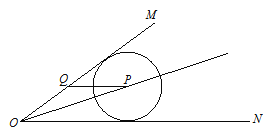
A.4<r<12B.2<r<12C.4<r<8D.r>4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com