
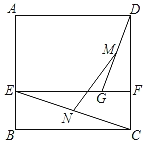
【题目】如图,已知正方形ABCD的边长为4,E,F分别为AB,CD边上的点,且EF∥BC,G为EF上一点,且GF=1,M,N分别为GD,EC的中点,则MN=_____.
【答案】![]()
【解析】
作MH⊥CD于H,NQ⊥CD于Q,MK⊥NQ于K,如图,先证明四边形BCFE为矩形得到EF=BC=4,再根据平行线分线段成比例定理得到![]() ,则MH=
,则MH=![]() ,DH=
,DH=![]() DF,同理可得NQ=2,CQ=
DF,同理可得NQ=2,CQ=![]() CF,则HQ=
CF,则HQ=![]() CD=2,易得四边形MKQH为矩形,则KQ=KH=
CD=2,易得四边形MKQH为矩形,则KQ=KH=![]() ,MK=HQ=2,然后在Rt△MNK中利用勾股定理计算MN的长.
,MK=HQ=2,然后在Rt△MNK中利用勾股定理计算MN的长.
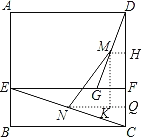
解:作MH⊥CD于H,NQ⊥CD于Q,MK⊥NQ于K,如图,
∵四边形ABCD为正方形,
∴∠BCD=90°,CB=CD=4,
∵EF∥BC,
∴EF⊥CD,
∴四边形BCFE为矩形,
∴EF=BC=4,
∴MH∥EF,NQ∥EF,
∵MH∥GF,
∵![]() ,M点为DG的中点,
,M点为DG的中点,
∴MH=![]() GF=
GF=![]() ,DH=
,DH=![]() DF,
DF,
同理可得NQ=![]() EF=2,CQ=
EF=2,CQ=![]() CF,
CF,
∴HQ=![]() (DF+CF)=
(DF+CF)=![]() CD=2,
CD=2,
易得四边形MKQH为矩形,
∴KQ=KH=![]() ,MK=HQ=2,
,MK=HQ=2,
∴NK=NQ﹣KQ=2﹣![]() =
=![]() ,
,
在Rt△MNK中,MN=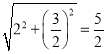 .
.
故答案为:![]() .
.


 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案科目:初中数学 来源: 题型:
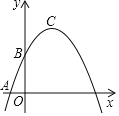
【题目】在平面直角坐标系xOy中(如图).已知抛物线y=﹣![]() x2+bx+c经过点A(﹣1,0)和点B(0,
x2+bx+c经过点A(﹣1,0)和点B(0,![]() ),顶点为C,点D在其对称轴上且位于点C下方,将线段DC绕点D按顺时针方向旋转90°,点C落在抛物线上的点P处.
),顶点为C,点D在其对称轴上且位于点C下方,将线段DC绕点D按顺时针方向旋转90°,点C落在抛物线上的点P处.
(1)求这条抛物线的表达式;
(2)求线段CD的长;
(3)将抛物线平移,使其顶点C移到原点O的位置,这时点P落在点E的位置,如果点M在y轴上,且以O、D、E、M为顶点的四边形面积为8,求点M的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AB=AC,以AC为直径的⊙O交BC于点![]() ,交AB于点E,点F为AC延长线上一点,且∠BAC=2∠CDF.
,交AB于点E,点F为AC延长线上一点,且∠BAC=2∠CDF.
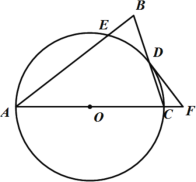
(1)求证:DF是⊙O的切线;
(2)连接DE,求证:DE=DB;
(3)若![]() ,CF=2,求⊙O的半径.
,CF=2,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
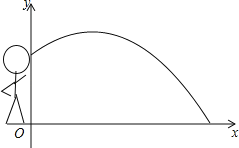
【题目】如图,一名运动员推铅球,已知铅球行进高度y(单位:m)与水平距离x(单位:m)之间的关系始终是y=ax2+![]() x+
x+![]() (a为常数,a<0).
(a为常数,a<0).
(1)解释上述函数表达式中“![]() ”的实际意义;
”的实际意义;
(2)当a=﹣![]() 时,这名运动员能把铅球推出多远?
时,这名运动员能把铅球推出多远?
(3)若这名运动员某次将铅球推出的距离不小于(2)中的距离,写出此时a的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于平面直角坐标系中的任意一点P(a,b),我们定义:当k为常数,且k≠0时,点P′(a+![]() ,ka+b)为点P的“k对应点”.
,ka+b)为点P的“k对应点”.
(1)点P(﹣2,1)的“3对应点”P′的坐标为 ;若点P的“﹣2对应点”P′的坐标为(﹣3,6),且点P的纵坐标为4,则点P的横坐标a= ;
(2)若点P的“k对应点”P′在第一、三象限的角平分线(原点除外)上,求k值;
(3)若点P在x轴的负半轴上,点P的“k对应点”为P′点,且∠OP'P=30°,求k值.
查看答案和解析>>
科目:初中数学 来源: 题型:
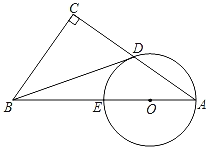
【题目】如图,在Rt△ABC中,∠C=90°,O在AB上,以O为圆心,以OA长为半径的圆分别与AC,AB交于点D,E,直线BD与⊙O相切于点 D.
(1)求证:∠CBD=∠A;
(2)若AC=6,AD:BC=1:![]() .
.
①求线段BD的长;
②求⊙O的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】新冠肺炎疫情期间,我市对学生进行了“停课不停学”的线上教学活动.某中学为了解这期间九年级学生数学学习的情况,开学后进行了两次诊断性练习.综合成绩由两次练习成绩组成,其中第一次练习成绩占40%,第二次练习成绩占60%.当综合成绩不低于135分时,该生数学学科综合评价为优秀.
(1)小明同学的两次练习成绩之和为260分,综合成绩为132分,则他这两次练习成绩各得多少分?
(2)如果小张同学第一次练习成绩为120分,综合成绩要达到优秀,他的第二次练习成绩至少要得多少分?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知在平面直角坐标系xOy中,抛物线y=ax2+bx+4经过点A(﹣3,0)和点B(3,2),与y轴相交于点C.
(1)求这条抛物线的表达式;
(2)点P是抛物线在第一象限内一点,联结AP,如果点C关于直线AP的对称点D恰好落在x轴上,求直线AP的截距;
(3)在(2)小题的条件下,如果点E是y轴正半轴上一点,点F是直线AP上一点.当△EAO与△EAF全等时,求点E的纵坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
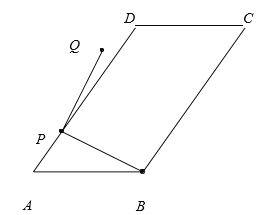
【题目】如图,在平行四边形ABCD中,AB=10,BC=15,tan∠A=![]() 点P为AD边上任意一点,连结PB,将PB绕点P逆时针旋转90°得到线段PQ.若点Q恰好落在平行四边形ABCD的边所在的直线上,则PB旋转到PQ所扫过的面积____(结果保留π)
点P为AD边上任意一点,连结PB,将PB绕点P逆时针旋转90°得到线段PQ.若点Q恰好落在平行四边形ABCD的边所在的直线上,则PB旋转到PQ所扫过的面积____(结果保留π)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com