
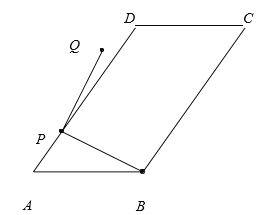
【题目】如图,在平行四边形ABCD中,AB=10,BC=15,tan∠A=![]() 点P为AD边上任意一点,连结PB,将PB绕点P逆时针旋转90°得到线段PQ.若点Q恰好落在平行四边形ABCD的边所在的直线上,则PB旋转到PQ所扫过的面积____(结果保留π)
点P为AD边上任意一点,连结PB,将PB绕点P逆时针旋转90°得到线段PQ.若点Q恰好落在平行四边形ABCD的边所在的直线上,则PB旋转到PQ所扫过的面积____(结果保留π)
【答案】![]() 或
或![]() 或
或![]()
【解析】
分三种情况:点Q在直线AD上,点Q在直线CD上和点Q在直线BC上,分别求出PB的长度,然后利用扇形的面积公式即可求解.
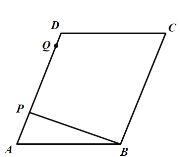
①当点Q在直线AD上时,此时![]() ,如图,
,如图,
![]() ,
,
![]() .
.
∵![]() ,
,
![]() .
.
![]() ,
,
![]() ,
,
∴PB旋转到PQ所扫过的面积为![]() ;
;
②当点Q在直线CD上时,此时![]() ,如图,
,如图,
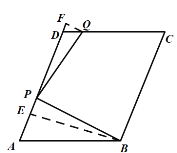
过点B作![]() 交AD于点E,过点Q作
交AD于点E,过点Q作![]() 交AD的延长线于点F,
交AD的延长线于点F,
∵四边形ABCD是平行四边形,
∴![]() ,
,
![]() .
.
![]() ,
,
![]() .
.
![]() ,
,
![]() .
.
在![]() 和
和![]() 中,
中,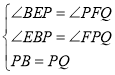
![]() ,
,
![]() .
.
由①知,![]() ,
,
设![]() ,
,
则![]() .
.
![]() ,
,
![]() ,
,
解得![]() ,
,
![]() ,
,
![]() ,
,
∴PB旋转到PQ所扫过的面积为![]() ;
;
③当点Q在直线BC上时,此时![]() ,如图,
,如图,
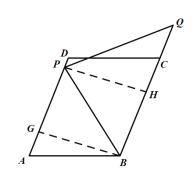
过点B作![]() 交AD于点E,过点P作
交AD于点E,过点P作![]() 交BC于点H,
交BC于点H,
∵四边形ABCD是平行四边形,
∴![]() .
.
∵![]() ,
,![]() ,
,
![]() ,
,
∴四边形BGPH是平行四边形.
∵![]() ,
,
∴四边形BGPH是矩形,
∴![]() .
.
![]() ,
,
![]() ,
,
![]() ,
,
∴PB旋转到PQ所扫过的面积为![]() ;
;
故答案为:![]() 或
或![]() 或
或![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c(a≠0)的图象如图所示,其对称轴为直线x=﹣1,与x轴的交点为(x1,0)、(x2,0),其中0<x2<1,有下列结论:①b2﹣4ac>0;②4a﹣2b+c>﹣1;③﹣3<x1<﹣2;④当m为任意实数时,a﹣b≤am2+bm;⑤3a+c=0.其中,正确的结论有( )
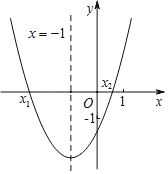
A.②③④B.①③⑤C.②④⑤D.①③④
查看答案和解析>>
科目:初中数学 来源: 题型:
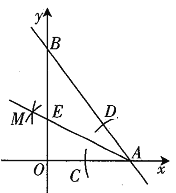
【题目】如图,![]() 的直角边
的直角边![]() 在x轴上,
在x轴上,![]() 在y轴的正半轴上,且
在y轴的正半轴上,且![]() ,
,![]() ,按以下步骤作图:①以点A为圆心,适当长度为半径作弧,分别交
,按以下步骤作图:①以点A为圆心,适当长度为半径作弧,分别交![]() ,
,![]() 于点C,D;②分别以C,D为圆心,大于
于点C,D;②分别以C,D为圆心,大于![]() 的长为半径作弧,两弧在
的长为半径作弧,两弧在![]() 内交于点M;③作射线
内交于点M;③作射线![]() ,交y轴于点E,则点E的坐标为( )
,交y轴于点E,则点E的坐标为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】黄石市在创建国家级文明卫生城市中,绿化档次不断提升.某校计划购进A,B两种树木共100棵进行校园绿化升级,经市场调查:购买A种树木2棵,B种树木5棵,共需600元;购买A种树木3棵,B种树木1棵,共需380元.
(1)求A种,B种树木每棵各多少元?
(2)因布局需要,购买A种树木的数量不少于B种树木数量的3倍.学校与中标公司签订的合同中规定:在市场价格不变的情况下(不考虑其他因素),实际付款总金额按市场价九折优惠,请设计一种购买树木的方案,使实际所花费用最省,并求出最省的费用.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,CD是⊙O的直径,OB⊥CD交⊙O于点B,连接CB,AB是⊙O的弦,AB交CD于点E,F是CD的延长线上一点且AF=EF.

(1)判断AF和⊙O的位置关系并说明理由.
(2)若∠ABC=60°,BC=1cm,求阴影部分的面积.(结果保留根号).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在矩形ABCD中,AB=5,BC=4,E是BC边上一点,连接DE,将矩形ABCD沿DE折叠,顶点C恰好落在AB边上点F处,延长DE交AB的延长线于点G.
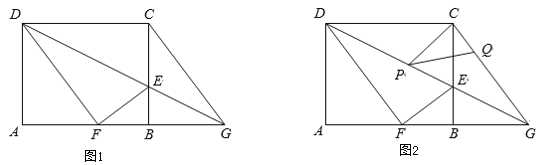
(1)求线段BE的长;
(2)连接CG,求证:四边形CDFG是菱形;
(3)如图2,P,Q分别是线段DG,CG上的动点(与端点不重合),且∠CPQ=∠CDP,是否存在这样的点P,使△CPQ是等腰三角形?若存在,请直接写出DP的值,若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
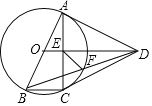
【题目】如图,四边形ABCD中,AB=AD=CD,以AB为直径的⊙O经过点C,连接AC,OD交于点E.
(1)证明:OD∥BC;
(2)若tan∠ABC=2,证明:DA与⊙O相切;
(3)在(2)条件下,连接BD交于⊙O于点F,连接EF,若BC=1,求EF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
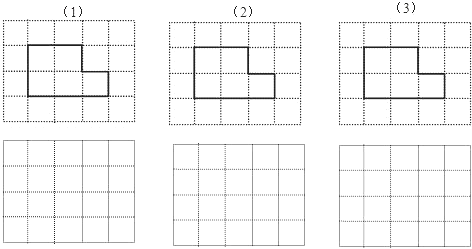
【题目】现有一块形如母子正方形的板材,木工师傅想先把它分割成几块,然后适当拼接,制成某种特殊形状的板面(要求板材不能有剩余,拼接时不重叠、无空隙),请你按下列要求,帮助木工师傅分别设计一种方案:
(1)板面形状为非正方形的中心对称图形;
(2)板面形状为等腰梯形;
(3)板面形状为正方形.
请在方格纸中的图形上画出分割线,在相应的下边的方格纸上面画出拼接后的图形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在△ABC中,C90,点D是AB边上一点,以BD为直径的⊙O与边AC相切于点E,与边BC交于点F,过点E作EHAB于点H,连结BE.
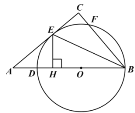
(1)求证:BCBH;
(2)若AB5,AC4,求CE的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com