
����Ŀ����ͼ����֪��ƽ��ֱ������ϵxOy�У�������y��ax2+bx+4������A����3��0���͵�B��3��2������y���ཻ�ڵ�C��
��1�������������ߵı���ʽ��
��2����P���������ڵ�һ������һ�㣬����AP�������C����ֱ��AP�ĶԳƵ�Dǡ������x���ϣ���ֱ��AP�Ľؾࣻ
��3���ڣ�2��С��������£������E��y����������һ�㣬��F��ֱ��AP��һ�㣮����EAO���EAFȫ��ʱ�����E�������꣮
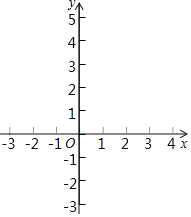
���𰸡���1��![]() ����2��
����2��![]() ����3��
����3��![]() ��3
��3![]() ��6
��6
��������
��1����![]() �͵�
�͵�![]() ���������ߵĽ���ʽ���з����飬�ɵý��ۣ�
���������ߵĽ���ʽ���з����飬�ɵý��ۣ�
��2����ͼ1�����ݶԳƵ����ʵ�![]() ���ɵ�
���ɵ�![]() ����
����![]() ����
����![]() ����
����![]() �У����ݹ��ɶ�����
�У����ݹ��ɶ�����![]() ���з��̿ɵý��ۣ�
���з��̿ɵý��ۣ�
��3���������������˵��![]() ��ֱ�������Σ�����
��ֱ�������Σ�����![]() Ҳ��ֱ�������Σ�����
Ҳ��ֱ�������Σ�����![]() ����ͼ���ɹ��ɶ����з��̿ɽ��
����ͼ���ɹ��ɶ����з��̿ɽ��
�⣺��1��![]() ������
������![]() ����
����![]() �͵�
�͵�![]() ��
��
![]()
![]() ��
��
��� ��
��
![]()
![]() ��
��
��2����ͼ1������![]() ��
��![]() ��
��
![]() ��
��![]() ����ֱ��
����ֱ��![]() �ĶԳƵ�
�ĶԳƵ�![]() ��
��
![]() ��
��
![]()
![]() ��
��![]() �ύ�ڵ�
�ύ�ڵ�![]() ����
����![]() �ύ�ڵ�
�ύ�ڵ�![]() ��
��
![]() ��
��
![]() ��
��
![]() ��
��![]() ��
��
��ֱ��![]() ��
��![]() �ύ�ڵ�
�ύ�ڵ�![]() ����
����![]() ��
��

��![]() ����
����![]() ��
��
��![]() ��
��![]() ��
��
![]() ��
��
![]()
![]() ��
��
![]() ֱ��
ֱ��![]() �Ľؾ�Ϊ
�Ľؾ�Ϊ![]() ��
��
��3��![]() ��
��![]() ��
��![]() ����������һ�㣬
����������һ�㣬
![]() ��ֱ�������Σ���
��ֱ�������Σ���![]()
��![]() ��
��![]() ȫ��ʱ���������������
ȫ��ʱ���������������
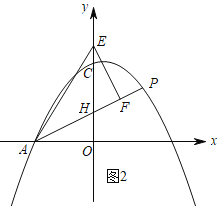
����ͼ2����![]() ��
��![]() ��
��
![]() ��
��
![]() ��
��![]() ��
��
![]() ��
��
![]() ��
��
�ɣ�2��֪��![]() ��
��
![]() ��
��
![]() �У�
��![]() ��
��
![]() ��
��
��ã�![]() ��
��![]() ����
����![]() ��
��
![]() ��
��![]() ����������
����������![]() ��
��
����ͼ3����![]() ��
��![]() ��
��

![]() ��
��![]() ��
��
![]() �У�
��![]() ��
��
![]() ��
��![]() ��
��
![]() �У��ɹ��ɶ����ã�
�У��ɹ��ɶ����ã�![]() ��
��
![]() ��
��
��ã�![]() ��
��
![]() ��
��![]() ����������
����������![]() ��
��
���ϣ���![]() ����������
����������![]() ��
��![]() ��
��


 ��ĩ���100�ִ��½����ȫ�Ծ�ϵ�д�
��ĩ���100�ִ��½����ȫ�Ծ�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
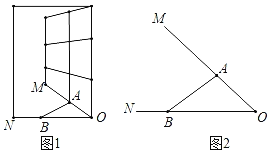
����Ŀ����ͼ1��һ�ȴ�����һ���Ƕȣ�����һ�˹̶��ڴ�����OM�ϵĵ�A������һ��B�ڱ�ON�ϻ�����ͼ2Ϊijһλ�ô������¿���ƽ��ͼ����á�ABOΪ37������AOBΪ45����OB��Ϊ35���ף���AB�ij����ο����ݣ�sin37���0.6��cos37���0.8��tan37���0.75��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
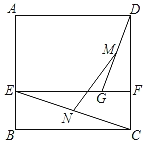
����Ŀ����ͼ����֪������ABCD�ı߳�Ϊ4��E��F�ֱ�ΪAB��CD���ϵĵ㣬��EF��BC��GΪEF��һ�㣬��GF=1��M��N�ֱ�ΪGD��EC���е㣬��MN=_____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�ֱ��![]() �ֱ���x��y�ύ��A��B���㣬��ֱ��AB����y�ᷭ�ۣ���x�Ḻ�����ڵ�C��
�ֱ���x��y�ύ��A��B���㣬��ֱ��AB����y�ᷭ�ۣ���x�Ḻ�����ڵ�C��
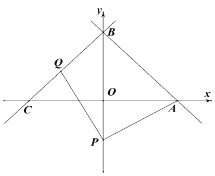
��1����ֱ��BC�ĺ�����ϵʽ��
��2����P��0��t����y�Ḻ�����ϣ�QΪ�߶�BC��һ���㣨����B��C�غϣ�������PA��PQ��PQ��PA
������QΪBC�е㣬��t��ֵ��
����t�Ĵ���ʽ��ʾ��Q�������ֱ��PQ�ĺ�����ϵʽ��
����M��2m��n��8����N��t3��2t2��2m��n����ֱ��PQ�ϣ���n��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪���ı���ABCD�У�AB��CD���Խ���AC��BD�ཻ�ڵ�O����ô�������������ж�����ı����Ǿ��ε��ǣ�������
A.AD��BC��AC��BDB.AC��BD����BAD����BCD
C.AO��CO��AB��BCD.AO��OB��AC��BD
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
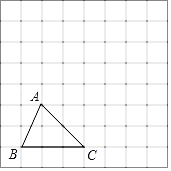
����Ŀ����ͼ������ֽ�е�ÿ��С�����DZ߳�Ϊ1����λ���ȵ������Σ�ÿ��С�����εĶ���и�㣬��ABC�Ķ�����ڸ���ϣ���Ҫ��������в��裺
��1����������ABC����ƽ��3����λ��õ��ġ�A1B1C1��
��2����������A1B1C1�Ƶ�C1��˳ʱ�뷽����ת90������õ��ġ�A2B2C1��
��3������ڣ�2������B1�㾭����·������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����MON=30����p�ǡ�MON�Ľ�ƽ���ߣ�PQƽ��ON��OM�ڵ�Q����PΪԲ�İ뾶Ϊ4��ԲON���У������QΪԲ�İ뾶Ϊr��Բ��![]() �ཻ����ôr��ȡֵ��Χ�ǣ� ��
�ཻ����ôr��ȡֵ��Χ�ǣ� ��
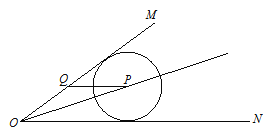
A.4<r<12B.2<r<12C.4<r<8D.r>4
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ���������ɫ�Ļ������к�ɫ�Ļ�����ijУ����֯ѧ����չ��ѧ������˽⣬��A����������ַ��B�����ӻ����ַ��C��¦ɽ�غ��ս����ַ��D���Ķɳ�ˮ����ݹ��ĸ���ѡ�����ѧ���أ��������ȡ����ѧ���Ի��ص�ѡ����е��飬ÿ�˱�����ֻ��ѡ��һ�����أ����ݵ������������²�����������ͳ��ͼ������ͳ��ͼ��

��1��ͳ��ͼ��m���� ����n���� ����
��2������У��1500��ѧ���������ѡ��B���ص�ѧ��������
��3��ij����ѡ��B���ص�4��ѧ������2����ͬѧ��2��Ůͬѧ����������ѡ��2��ͬѧ���Ρ�С���Ρ���������״ͼ���оٷ�����2��ͬѧǡ����һ��һŮ�ĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ���ı���ABCD�У�BE��DF�ֱ���ƽ���ı��ε�������ǵ�ƽ���ߣ���EAF��![]() ��BAD����AE��AF�ֱ�������ƽ�����ڵ�E��F��
��BAD����AE��AF�ֱ�������ƽ�����ڵ�E��F��
��1����֤����ABE�ס�FDA��
��2������BD��EF�����DF2��ADAB����֤��BD��EF��

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com