
【题目】为弘扬遵义红色文化,传承红色文化精神,某校准备组织学生开展研学活动.经了解,有A.遵义会议会址、B.苟坝会议会址、C.娄山关红军战斗遗址、D.四渡赤水纪念馆共四个可选择的研学基地.现随机抽取部分学生对基地的选择进行调查,每人必须且只能选择一个基地.根据调查结果绘制如下不完整的条形统计图和扇形统计图.

(1)统计图中m= ,n= ;
(2)若该校有1500名学生,请估计选择B基地的学生人数;
(3)某班在选择B基地的4名学生中有2名男同学和2名女同学,需从中随机选出2名同学担任“小导游”,请用树状图或列举法求这2名同学恰好是一男一女的概率.
【答案】(1)56,15;(2)555人;(3)![]() .
.
【解析】
(1)先由C类别人数及其所占百分比求出总人数,再进一步求解可得;
(2)用总人数乘以样本中选择B基地的学生人数所占比例即可得;
(3)根据题意画出树状图得出所有等情况数,找出选出的2名学生恰好是一男一女的情况数,然后根据概率公式即可得出答案.
解:(1)由题意可知:总人数为40÷20%=200(人)
所以m=200×28%=56(人),n%=![]() ×100%=15%,即n=15,
×100%=15%,即n=15,
故答案为:56,15;
(2)估计选择B基地的学生人数1500×![]() =555(人);
=555(人);
(3)根据题意画出树状图如下:
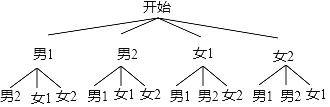
一共有12种情况,恰好是1男1女的情况有8种,
∴这2名同学恰好是一男一女的概率为![]() =
=![]() .
.


科目:初中数学 来源: 题型:
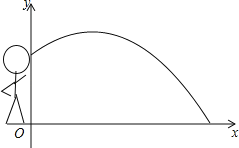
【题目】如图,一名运动员推铅球,已知铅球行进高度y(单位:m)与水平距离x(单位:m)之间的关系始终是y=ax2+![]() x+
x+![]() (a为常数,a<0).
(a为常数,a<0).
(1)解释上述函数表达式中“![]() ”的实际意义;
”的实际意义;
(2)当a=﹣![]() 时,这名运动员能把铅球推出多远?
时,这名运动员能把铅球推出多远?
(3)若这名运动员某次将铅球推出的距离不小于(2)中的距离,写出此时a的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知在平面直角坐标系xOy中,抛物线y=ax2+bx+4经过点A(﹣3,0)和点B(3,2),与y轴相交于点C.
(1)求这条抛物线的表达式;
(2)点P是抛物线在第一象限内一点,联结AP,如果点C关于直线AP的对称点D恰好落在x轴上,求直线AP的截距;
(3)在(2)小题的条件下,如果点E是y轴正半轴上一点,点F是直线AP上一点.当△EAO与△EAF全等时,求点E的纵坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中(如图),已知抛物线![]() 经过点
经过点![]() 和
和![]() ,其顶点为C.
,其顶点为C.

(1)求抛物线的解析式和顶点C的坐标;
(2)我们把坐标为(n,m)的点叫做坐标为(m,n)的点的反射点,已知点M在这条抛物线上,它的反射点在抛物线的对称轴上,求点M的坐标;
(3)点P是抛物线在第一象限部分上的一点,如果∠POA=∠ACB,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为落实疫情期间的垃圾分类,树立全面环保意识,某校举行了“垃圾分类,绿色环保”知识竞赛活动,根据学生的成绩划分为![]() ,
,![]() ,
,![]() ,
,![]() 四个等级,并绘制了不完整的两种统计图:
四个等级,并绘制了不完整的两种统计图:
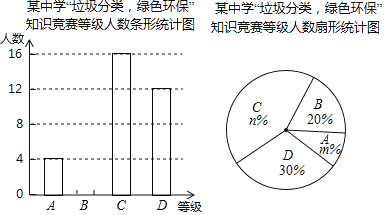
根据图中提供的信息,回答下列问题:
(1)参加知识竞赛的学生共有______人,并把条形统计图补充完整;
(2)扇形统计图中,![]() ______,
______,![]() ______,
______,![]() 等级对应的圆心角为______度;
等级对应的圆心角为______度;
(3)小明是四名获![]() 等级的学生中的一位,学校将从获
等级的学生中的一位,学校将从获![]() 等级的学生中任选取2人,参加市举办的知识竞赛,请用列表法或画树状图,求小明被选中参加区知识竞赛的概率.
等级的学生中任选取2人,参加市举办的知识竞赛,请用列表法或画树状图,求小明被选中参加区知识竞赛的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】据交管部门统计,高速公路超速行驶是引发交通事故的主要原因.我县某校数学课外小组的几个同学想尝试用自己所学的知识检测车速,渝黔高速公路某路段的限速是:每小时80千米(即最高时速不超过80千米),如图,他们将观测点设在到公路l的距离为0.1千米的P处.这时,一辆轿车由綦江向重庆匀速直线驶来,测得此车从A处行驶到B处所用的时间为3秒(注:3秒=![]() 小时),并测得∠APO=59°,∠BPO=45°.试计算AB并判断此车是否超速?(精确到0.001).(参考数据:sin59°≈0.8572,cos59°≈0.5150,tan59°≈1.6643)
小时),并测得∠APO=59°,∠BPO=45°.试计算AB并判断此车是否超速?(精确到0.001).(参考数据:sin59°≈0.8572,cos59°≈0.5150,tan59°≈1.6643)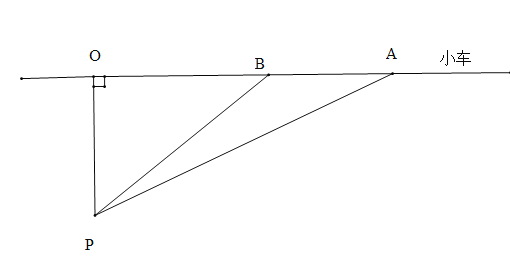
查看答案和解析>>
科目:初中数学 来源: 题型:
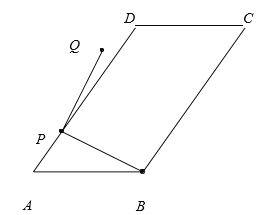
【题目】如图,在平行四边形ABCD中,AB=10,BC=15,tan∠A=![]() 点P为AD边上任意一点,连结PB,将PB绕点P逆时针旋转90°得到线段PQ.若点Q恰好落在平行四边形ABCD的边所在的直线上,则PB旋转到PQ所扫过的面积____(结果保留π)
点P为AD边上任意一点,连结PB,将PB绕点P逆时针旋转90°得到线段PQ.若点Q恰好落在平行四边形ABCD的边所在的直线上,则PB旋转到PQ所扫过的面积____(结果保留π)
查看答案和解析>>
科目:初中数学 来源: 题型:
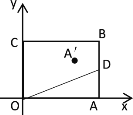
【题目】如图,在平面直角坐标系中,矩形![]() 的点
的点![]() 坐标为
坐标为![]() ,点
,点![]() 在
在![]() 轴上,点
轴上,点![]() 在
在![]() 轴上.点
轴上.点![]() 是边
是边![]() 上的动点,连接
上的动点,连接![]() ,作点
,作点![]() 关于线段
关于线段![]() 的对称点
的对称点![]() .已知一条抛物线
.已知一条抛物线![]() 经过
经过![]() 三点,且点
三点,且点![]() 恰好是抛物线的顶点,则
恰好是抛物线的顶点,则![]() 的值为()
的值为()
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,双曲线![]() 与直线
与直线![]() 相交于
相交于![]() ,点P是x轴上一动点.
,点P是x轴上一动点.
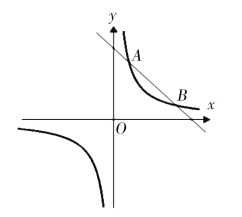
(1)求双曲线![]() 与直线
与直线![]() 的解析式;
的解析式;
(2)当![]() 时,直接写出x的取值范围;
时,直接写出x的取值范围;
(3)当![]() 是等腰三角形时,求点P的坐标.
是等腰三角形时,求点P的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com