
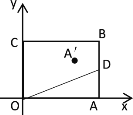
【题目】如图,在平面直角坐标系中,矩形![]() 的点
的点![]() 坐标为
坐标为![]() ,点
,点![]() 在
在![]() 轴上,点
轴上,点![]() 在
在![]() 轴上.点
轴上.点![]() 是边
是边![]() 上的动点,连接
上的动点,连接![]() ,作点
,作点![]() 关于线段
关于线段![]() 的对称点
的对称点![]() .已知一条抛物线
.已知一条抛物线![]() 经过
经过![]() 三点,且点
三点,且点![]() 恰好是抛物线的顶点,则
恰好是抛物线的顶点,则![]() 的值为()
的值为()
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线![]() 分别与x、y轴交于A、B两点,将直线AB沿着y轴翻折,交x轴负半轴于点C.
分别与x、y轴交于A、B两点,将直线AB沿着y轴翻折,交x轴负半轴于点C.
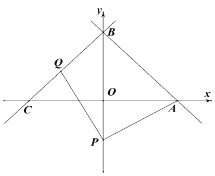
(1)求直线BC的函数关系式;
(2)点P(0,t)在y轴负半轴上,Q为线段BC上一动点(不与B、C重合).连接PA、PQ,PQ=PA
①若点Q为BC中点,求t的值;
②用t的代数式表示点Q的坐标和直线PQ的函数关系式;
③若M(2m,n-8),N(t3+2t2-2m,n)在直线PQ上,求n的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为弘扬遵义红色文化,传承红色文化精神,某校准备组织学生开展研学活动.经了解,有A.遵义会议会址、B.苟坝会议会址、C.娄山关红军战斗遗址、D.四渡赤水纪念馆共四个可选择的研学基地.现随机抽取部分学生对基地的选择进行调查,每人必须且只能选择一个基地.根据调查结果绘制如下不完整的条形统计图和扇形统计图.

(1)统计图中m= ,n= ;
(2)若该校有1500名学生,请估计选择B基地的学生人数;
(3)某班在选择B基地的4名学生中有2名男同学和2名女同学,需从中随机选出2名同学担任“小导游”,请用树状图或列举法求这2名同学恰好是一男一女的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工厂制作![]() 两种手工艺品,
两种手工艺品,![]() 每天每件获利比
每天每件获利比![]() 多105元,获利30元的
多105元,获利30元的![]() 与获利240元的
与获利240元的![]() 数量相等.
数量相等.
(1)制作一件![]() 和一件
和一件![]() 分别获利多少元?
分别获利多少元?
(2)工厂安排65人制作![]() ,
,![]() 两种手工艺品,每人每天制作2件
两种手工艺品,每人每天制作2件![]() 或1件
或1件![]() .现在在不增加工人的情况下,增加制作
.现在在不增加工人的情况下,增加制作![]() .已知每人每天可制作1件
.已知每人每天可制作1件![]() (每人每天只能制作一种手工艺品),要求每天制作
(每人每天只能制作一种手工艺品),要求每天制作![]() ,
,![]() 两种手工艺品的数量相等.设每天安排
两种手工艺品的数量相等.设每天安排![]() 人制作
人制作![]() ,
,![]() 人制作
人制作![]() ,写出
,写出![]() 与
与![]() 之间的函数关系式.
之间的函数关系式.
(3)在(1)(2)的条件下,每天制作![]() 不少于5件.当每天制作5件时,每件获利不变.若每增加1件,则当天平均每件获利减少2元.已知
不少于5件.当每天制作5件时,每件获利不变.若每增加1件,则当天平均每件获利减少2元.已知![]() 每件获利30元,求每天制作三种手工艺品可获得的总利润
每件获利30元,求每天制作三种手工艺品可获得的总利润![]() (元)的最大值及相应
(元)的最大值及相应![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
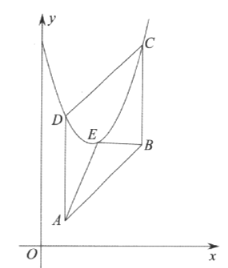
【题目】如图,在平面直角坐标系中,点![]() 是一次函数
是一次函数![]() 图象上两点,它们的横坐标分别为
图象上两点,它们的横坐标分别为![]() 其中
其中![]() ,过点
,过点![]() 分别作
分别作![]() 轴的平行线,交抛物线
轴的平行线,交抛物线![]() 于点
于点![]() ,
,![]()
(1)若![]() 求
求![]() 的值;
的值;
(2)点![]() 是抛物线上的一点,求
是抛物线上的一点,求![]() 面积的最小值.
面积的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,以点![]() 为旋转中心,将线段
为旋转中心,将线段![]() 按顺时针方向旋转
按顺时针方向旋转![]() 得到线段
得到线段![]() ,连结
,连结![]() .
.
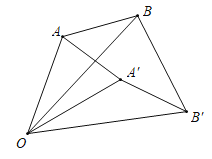
(1)比较![]() 与
与![]() 的大小,并说明理由.
的大小,并说明理由.
(2)当![]() 时,若
时,若![]() ,请你编制一个计算题(不标注新的字母),并解答
,请你编制一个计算题(不标注新的字母),并解答
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,BE、DF分别是平行四边形的两个外角的平分线,∠EAF=![]() ∠BAD,边AE、AF分别交两条角平分线于点E、F.
∠BAD,边AE、AF分别交两条角平分线于点E、F.
(1)求证:△ABE∽△FDA;
(2)联结BD、EF,如果DF2=ADAB,求证:BD=EF.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+c经过点B(4,0),C(0,﹣2),对称轴为直线x=1,与x轴的另一个交点为点A.

(1)求抛物线的解析式;
(2)点M从点A出发,沿AC向点C运动,速度为1个单位长度/秒,同时点N从点B出发,沿BA向点A运动,速度为2个单位长度/秒,当点M、N有一点到达终点时,运动停止,连接MN,设运动时间为t秒,当t为何值时,AMN的面积S最大,并求出S的最大值;
(3)点P在x轴上,点Q在抛物线上,是否存在点P、Q,使得以点P、Q、B、C为顶点的四边形是平行四边形,若存在,直接写出所有符合条件的点P坐标,若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解某中学学生课余生活情况,对喜爱看课外书、体育活动、看电视、社会实践四个方面的人数进行调查统计.现从该校随机抽取![]() 名学生作为样本,采用问卷调查的方法收集数据(参与问卷调查的每名学生只能选择其中一项).并根据调查得到的数据绘制成了如图所示的两幅不完整的统计图.由图中提供的信息,解答下列问题:
名学生作为样本,采用问卷调查的方法收集数据(参与问卷调查的每名学生只能选择其中一项).并根据调查得到的数据绘制成了如图所示的两幅不完整的统计图.由图中提供的信息,解答下列问题:
(1)求n的值;
(2)若该校学生共有1200人,试估计该校喜爱看电视的学生人数;
(3)若调查到喜爱体育活动的4名学生中有3名男生和1名女生,现从这4名学生中任意抽取2名学生,求恰好抽到2名男生的概率.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com