
【题目】如图,在平面直角坐标系中,直线![]() 分别与x、y轴交于A、B两点,将直线AB沿着y轴翻折,交x轴负半轴于点C.
分别与x、y轴交于A、B两点,将直线AB沿着y轴翻折,交x轴负半轴于点C.
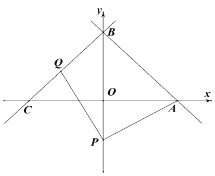
(1)求直线BC的函数关系式;
(2)点P(0,t)在y轴负半轴上,Q为线段BC上一动点(不与B、C重合).连接PA、PQ,PQ=PA
①若点Q为BC中点,求t的值;
②用t的代数式表示点Q的坐标和直线PQ的函数关系式;
③若M(2m,n-8),N(t3+2t2-2m,n)在直线PQ上,求n的取值范围.
【答案】(1)![]() ;(2)①t=-3,②
;(2)①t=-3,②![]() ,③-6<t<0,
,③-6<t<0,![]() ≤n<70
≤n<70
【解析】
(1)根据题意求出A,B的坐标,从而可得出C点的坐标,用待定系数法即可得出解析式;
(2)①首先根据Q为BC中点,得出Q的坐标,然后过Q点作QE⊥y轴,可得QE=3,EP=3-t,OP=|t|,OA=6,然后根据PQ=PA和勾股定理,可得![]() =
=![]() ,求解即可;
,求解即可;
②设Q(a,a+6),由题意得:![]() ,解出方程求出Q的坐标为(t,t+6),然后利用待定系数法求出解析式即可;
,解出方程求出Q的坐标为(t,t+6),然后利用待定系数法求出解析式即可;
③将M(2m,n-8),N(t3+2t2-2m,n)代入PQ的函数关系式得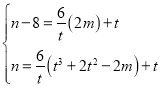 ,然后消去m得n=3t2+7t+4,在根据t的取值范围即可推出,n的取值范围.
,然后消去m得n=3t2+7t+4,在根据t的取值范围即可推出,n的取值范围.
(1)∵直线![]() 分别与x、y轴交于A、B两点,
分别与x、y轴交于A、B两点,
∴可得A(6,0),B(0,6),
∵点C和点A关于x轴对称,
∴C(-6,0),
设BC的解析式为y=kx+b,
将B,C两点代入得![]() ,
,
解得:k=1,b=6,
∴BC的解析式为:![]() ;
;
(2)①∵Q为BC中点,
∴Q的坐标为(-3,3),
过Q点作QE⊥y轴,
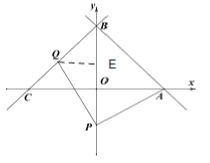
∴E的坐标为(0,3),
∴QE=3,EP=3-t,OP=|t|,OA=6,
∵PQ=PA,
∴![]() =
=![]() ,
,
即![]() =
=![]() ,
,
解得t=-3;
②设Q(a,a+6),
由题意得:![]() ,
,
解得![]() ,
,![]() (舍),
(舍),
∴Q(t,t+6),
设直线PQ函数关系式为y=kx+b,
将Q,P代入得![]() ,
,
解得![]() ,
,
∴直线PQ函数关系式为![]() ;
;
③∵点M(2m,n-8),N(t3+2t2-2m,n)在直线PQ上,
由②可得PQ函数关系式为![]() ,
,
∴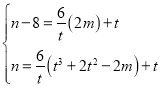 ,
,
消去m得n=3t2+7t+4,
∵Q为线段BC上一动点(不与B、C重合),
∴-6<t<0,
∵n=3t2+7t+4,
∴对称轴为t=![]() ,
,
∴n的最小值为:n=3×![]() -7×
-7×![]() +4=
+4=![]() ,
,
当t=-6时,n=3×36-7×6+4=70,
当t=0时,n=4,
∴n的取值范围是:![]() ≤n<70.
≤n<70.


 浙大优学小学年级衔接捷径浙江大学出版社系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案科目:初中数学 来源: 题型:
【题目】某超市为庆祝开业举办大酬宾抽奖活动,凡在开业当天进店购物的顾客,都能获得一次抽奖的机会,抽奖规则如下:在一个不透明的盒子里装有分别标有数字1、2、3、4的4个小球,它们的形状、大小、质地完全相同,顾客先从盒子里随机取出一个小球,记下小球上标有的数字,然后把小球放回盒子并搅拌均匀,再从盒子中随机取出一个小球,记下小球上标有的数字,并计算两次记下的数字之和,若两次所得的数字之和为8,则可获得50元代金券一张;若所得的数字之和为6,则可获得30元代金券一张;若所得的数字之和为5,则可获得15元代金券一张;其他情况都不中奖.
(1)请用列表或树状图(树状图也称树形图)的方法(选其中一种即可),把抽奖一次可能出现的结果表示出来;
(2)假如你参加了该超市开业当天的一次抽奖活动,求能中奖的概率P.
查看答案和解析>>
科目:初中数学 来源: 题型:
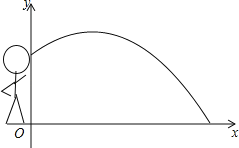
【题目】如图,一名运动员推铅球,已知铅球行进高度y(单位:m)与水平距离x(单位:m)之间的关系始终是y=ax2+![]() x+
x+![]() (a为常数,a<0).
(a为常数,a<0).
(1)解释上述函数表达式中“![]() ”的实际意义;
”的实际意义;
(2)当a=﹣![]() 时,这名运动员能把铅球推出多远?
时,这名运动员能把铅球推出多远?
(3)若这名运动员某次将铅球推出的距离不小于(2)中的距离,写出此时a的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
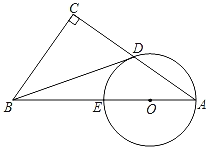
【题目】如图,在Rt△ABC中,∠C=90°,O在AB上,以O为圆心,以OA长为半径的圆分别与AC,AB交于点D,E,直线BD与⊙O相切于点 D.
(1)求证:∠CBD=∠A;
(2)若AC=6,AD:BC=1:![]() .
.
①求线段BD的长;
②求⊙O的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】新冠肺炎疫情期间,我市对学生进行了“停课不停学”的线上教学活动.某中学为了解这期间九年级学生数学学习的情况,开学后进行了两次诊断性练习.综合成绩由两次练习成绩组成,其中第一次练习成绩占40%,第二次练习成绩占60%.当综合成绩不低于135分时,该生数学学科综合评价为优秀.
(1)小明同学的两次练习成绩之和为260分,综合成绩为132分,则他这两次练习成绩各得多少分?
(2)如果小张同学第一次练习成绩为120分,综合成绩要达到优秀,他的第二次练习成绩至少要得多少分?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中(如图),已知经过点A(﹣3,0)的抛物线y=ax2+2ax﹣3与y轴交于点C,点B与点A关于该抛物线的对称轴对称,D为该抛物线的顶点.
(1)直接写出该抛物线的对称轴以及点B的坐标、点C的坐标、点D的坐标;
(2)联结AD、DC、CB,求四边形ABCD的面积;
(3)联结AC.如果点E在该抛物线上,过点E作x轴的垂线,垂足为H,线段EH交线段AC于点F.当EF=2FH时,求点E的坐标.
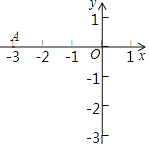
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知在平面直角坐标系xOy中,抛物线y=ax2+bx+4经过点A(﹣3,0)和点B(3,2),与y轴相交于点C.
(1)求这条抛物线的表达式;
(2)点P是抛物线在第一象限内一点,联结AP,如果点C关于直线AP的对称点D恰好落在x轴上,求直线AP的截距;
(3)在(2)小题的条件下,如果点E是y轴正半轴上一点,点F是直线AP上一点.当△EAO与△EAF全等时,求点E的纵坐标.
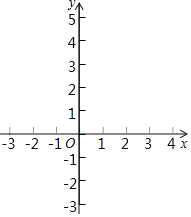
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中(如图),已知抛物线![]() 经过点
经过点![]() 和
和![]() ,其顶点为C.
,其顶点为C.

(1)求抛物线的解析式和顶点C的坐标;
(2)我们把坐标为(n,m)的点叫做坐标为(m,n)的点的反射点,已知点M在这条抛物线上,它的反射点在抛物线的对称轴上,求点M的坐标;
(3)点P是抛物线在第一象限部分上的一点,如果∠POA=∠ACB,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
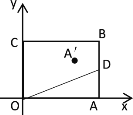
【题目】如图,在平面直角坐标系中,矩形![]() 的点
的点![]() 坐标为
坐标为![]() ,点
,点![]() 在
在![]() 轴上,点
轴上,点![]() 在
在![]() 轴上.点
轴上.点![]() 是边
是边![]() 上的动点,连接
上的动点,连接![]() ,作点
,作点![]() 关于线段
关于线段![]() 的对称点
的对称点![]() .已知一条抛物线
.已知一条抛物线![]() 经过
经过![]() 三点,且点
三点,且点![]() 恰好是抛物线的顶点,则
恰好是抛物线的顶点,则![]() 的值为()
的值为()
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com