
����Ŀ����ͼ��������y��ax2+bx+c������B(4��0)��C(0����2)���Գ���Ϊֱ��x��1����x�����һ������Ϊ��A��

��1���������ߵĽ���ʽ��
��2����M�ӵ�A��������AC���C�˶����ٶ�Ϊ1����λ����/�룬ͬʱ��N�ӵ�B��������BA���A�˶����ٶ�Ϊ2����λ����/�룬����M��N��һ�㵽���յ�ʱ���˶�ֹͣ������MN�����˶�ʱ��Ϊt�룬��tΪ��ֵʱ��AMN�����S������S�����ֵ��
��3����P��x���ϣ���Q���������ϣ��Ƿ���ڵ�P��Q��ʹ���Ե�P��Q��B��CΪ������ı�����ƽ���ı��Σ������ڣ�ֱ��д�����з��������ĵ�P���꣬�������ڣ���˵�����ɣ�
���𰸡���1��![]() ����2����
����2����![]() ʱ��S���ֵΪ
ʱ��S���ֵΪ![]() ����3�����ڣ�P1(��3+
����3�����ڣ�P1(��3+![]() ��0)��P2(��3��
��0)��P2(��3��![]() ��0)��P3(6��0)��P4(2��0)
��0)��P3(6��0)��P4(2��0)
��������
��1�����ô���ϵ����ȷ����������ʽ��
��2���������ߵĶԳ��������A��-2��0������AB=6������N�˶�t��ʱ��BN=2t����AN=6-2t������M��MD��x���ڵ�D������ֱ�������Σ��������ε������ʽ�г�������ϵʽ�������䷽��������ֵ��
��3����Ҫ������������ۣ���ƽ�Ƶ�֪ʶ�������Q�ĺ����꣬Ȼ���Ƴ���P�����꣮
��1�������⣬��B��4��0����C��0����2�����Գ���Ϊֱ��x��1�����������߽���ʽ��
��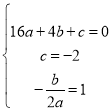 ��
��
��ã� ��
��
�������ߵĽ���ʽΪ��![]() ��
��
��2���߶Գ���Ϊֱ��x��1��B��4��0����
��A����2��0������AB��6��
����N�˶�t��ʱ��BN��2t����AN��6��2t��
��ͼ1������M��MD��x���ڵ�D��

��OA��OC��2��
���OAC�ǵ���ֱ�������Σ�
���OAC��45����
�֡�DM��OA��
���DAM�ǵ���ֱ�������Σ�AD��DM��
����M�˶�t��ʱ��AM��t��
��MD2+AD2��AM2��t2��
��DM��![]() ��
��
��![]() ��
��
��![]() ��
��
���ɶ��κ�����ͼ�����ʿ�֪����![]() ʱ��S���ֵΪ
ʱ��S���ֵΪ![]() ��
��
��3�����ڣ��������£�
�ٵ��ı���CBQPΪƽ���ı���ʱ��CB��PQƽ������ȣ�
��B��4��0����C��0����2����
��yB��yC��yQ��yP��2��xB��xC��xQ��xP��4��
��yP��0��
��yQ��2��
��y��2����![]() ��
��
�� x1��![]() ��x2��
��x2��![]() ��
��
�൱xQ��![]() ʱ��xP��
ʱ��xP��![]() ����xQ��
����xQ��![]() ʱ��xP��
ʱ��xP��![]() ��
��
��P1��![]() ��0����P2��
��0����P2��![]() ��0����
��0����
�ڵ��ı���CQPBΪƽ���ı���ʱ��BP��CQƽ������ȣ�
��yP��yB��0��
��yQ��yC����2��
��y����2����![]() ��
��
�� x1��0����ȥ����x2��2��
��xQ��2ʱ��
��xP��xB��xQ��xC��2��
��xP��6��
��P3��6��0����
�۵��ı���CQBPΪƽ���ı���ʱ��BP��CQƽ������ȣ�
�ɢ�֪��xQ��2��
��xB��xP��xQ��xC��2��
��xP��2��
��P4��2��0����
�����������������������ĵ�P��4�����ֱ���P1����3+![]() ��0����P2����3��
��0����P2����3��![]() ��0����P3��6��0����P4��2��0����
��0����P3��6��0����P4��2��0����



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵxOy�У���ͼ������֪������![]() ������
������![]() ��
��![]() ���䶥��ΪC��
���䶥��ΪC��

��1���������ߵĽ���ʽ�Ͷ���C�����ꣻ
��2�����ǰ�����Ϊ��n��m���ĵ��������Ϊ��m��n���ĵ�ķ���㣬��֪��M�������������ϣ����ķ�����������ߵĶԳ����ϣ����M�����ꣻ
��3����P���������ڵ�һ�������ϵ�һ�㣬�����POA=��ACB�����P�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�����![]() �ĵ�
�ĵ�![]() ����Ϊ
����Ϊ![]() ����
����![]() ��
��![]() ���ϣ���
���ϣ���![]() ��
��![]() ���ϣ���
���ϣ���![]() �DZ�
�DZ�![]() �ϵĶ��㣬����
�ϵĶ��㣬����![]() ������
������![]() �����߶�
�����߶�![]() �ĶԳƵ�
�ĶԳƵ�![]() ����֪һ��������
����֪һ��������![]() ����
����![]() ���㣬�ҵ�
���㣬�ҵ�![]() ǡ���������ߵĶ��㣬��
ǡ���������ߵĶ��㣬��![]() ��ֵΪ����
��ֵΪ����
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ʦΪ�˽�ͬѧ�ǶԽ�ӹ����С˵���Ķ����������Գ����꼶�IJ���ͬѧ���е��飬���������ֳ��������ࣺA������0��3����B������4��6����C������7��9����D������10��12����E������13��15��.�����ݵ�������������ͼ1��ͼ2������������ͳ��ͼ��
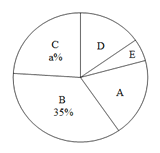
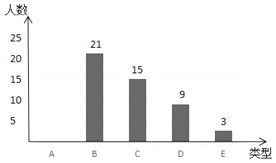
(1)ͼ2�е�a = ��D���Ե�Բ�ĽǶ���Ϊ �㣻
(2)�벹ȫ����ͳ��ͼ��
(3)���ε�����E����2��1Ů������ʦ����г�ȡ2��ͬѧ�ֱ�дһƪ����ʼ��������б�����״ͼ�ķ���������ȡ������ѧ��ǡ����һ��һŮ�ĸ�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����![]() ABCD�У���E��AD����һ�㣬AE��ED��1��2������AC��BE���ڵ�F.��S��AEF��1����S�ı���CDEF��_______.
ABCD�У���E��AD����һ�㣬AE��ED��1��2������AC��BE���ڵ�F.��S��AEF��1����S�ı���CDEF��_______.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ��һ�κ���y=k1x+8��ͼ����������ֱ�����ڵ�A��B�뷴����y=![]() ������ͼ���ཻ��C��D������C��CE��y�ᣬ����ΪE����CE=2��
������ͼ���ཻ��C��D������C��CE��y�ᣬ����ΪE����CE=2��
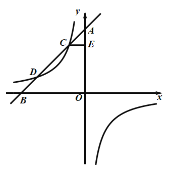
��1����4k1-k2��ֵ��
��2����CD=2AC�����������Ľ���ʽ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��˫����![]() ��ֱ��
��ֱ��![]() �ཻ��
�ཻ��![]() ����P��x����һ���㣮
����P��x����һ���㣮
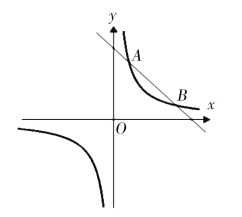
��1����˫����![]() ��ֱ��
��ֱ��![]() �Ľ���ʽ��
�Ľ���ʽ��
��2����![]() ʱ��ֱ��д��x��ȡֵ��Χ��
ʱ��ֱ��д��x��ȡֵ��Χ��
��3����![]() �ǵ���������ʱ�����P�����꣮
�ǵ���������ʱ�����P�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABC�ڽ��ڡ�O��ABΪֱ������OD��AB��AC�ڵ�D���ӳ�BC��OD���ڵ�F������C����O������CE����OF�ڵ�E��
��1����֤��EC��ED��
��2�����OA��4��EF��3������AC�ij���
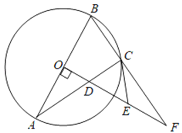
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1����һֱ��Ϊ100��Ħ���֣�����ߵ�������߶�Ϊ110�ף���Ħ��������ת��������ÿ����ת���ĽǶ���ͬ��һ�ܵ�ʱ��Ϊ24���ӣ�
��1����ͼ2��ij�ο����ڵ��մ���͵�P������3���Ӻ�A������ʱ���ο������߶�ԼΪ�����ף�����ȷ��������
��2�����ο���Ħ����ת��һ�ܵĹ����У��ж���ʱ�������治����85�ף����ο����ݣ�![]() ��1.41��
��1.41��![]() ��1.73��
��1.73��
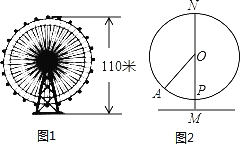
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com