
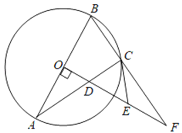
【题目】如图,△ABC内接于⊙O,AB为直径,作OD⊥AB交AC于点D,延长BC,OD交于点F,过点C作⊙O的切线CE,交OF于点E.
(1)求证:EC=ED;
(2)如果OA=4,EF=3,求弦AC的长.
【答案】(1)见解析;(2)![]()
【解析】
(1)连接OC,由切线的性质可证得∠ACE+∠A=90°,又∠CDE+∠A=90°,可得∠CDE=∠ACE,则结论得证;
(2)先根据勾股定理求出OE,OD,AD的长,证明Rt△AOD∽Rt△ACB,得出比例线段即可求出AC的长.
(1)证明:连接OC,
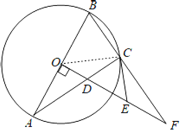
∵CE与⊙O相切,OC是⊙O的半径,
∴OC⊥CE,
∴∠OCA+∠ACE=90°,
∵OA=OC,
∴∠A=∠OCA,
∴∠ACE+∠A=90°,
∵OD⊥AB,
∴∠ODA+∠A=90°,
∵∠ODA=∠CDE,
∴∠CDE+∠A=90°,
∴∠CDE=∠ACE,
∴EC=ED;
(2)∵AB为⊙O的直径,
∴∠ACB=90°,
在Rt△DCF中,∠DCE+∠ECF=90°,∠DCE=∠CDE,
∴∠CDE+∠ECF=90°,
∵∠CDE+∠F=90°,
∴∠ECF=∠F,
∴EC=EF,
∵EF=3,
∴EC=DE=3,
∴OE=5,
∴OD=OE﹣DE=2,
在Rt△OAD中,AD=![]() ,
,
在Rt△AOD和Rt△ACB中,
∵∠A=∠A,∠ACB=∠AOD,
∴Rt△AOD∽Rt△ACB,
∴![]() ,即
,即![]() ,
,
∴AC=![]() .
.


 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,抛物线y=ax2+bx+c(a≠0)与x轴交于A,B两点(点A在点B的左侧),与y轴交于点C,点A的坐标为(﹣1,0),且OC=OB,tan∠OAC=4.
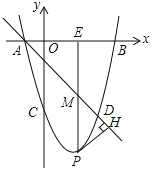
(1)求抛物线的解析式:
(2)若点D和点C关于抛物线的对称轴对称,直线AD下方的抛物线上有一点P,过点P作PH⊥AD于点H,作PM平行于y轴交直线AD于点M,交x轴于点E,求△PHM的周长的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,以
,以![]() 为直径的圆
为直径的圆![]() 交
交![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() ,以点
,以点![]() 为顶点作
为顶点作![]() ,使得
,使得![]() ,交
,交![]() 延长线于点
延长线于点![]() ,连接
,连接![]() 、
、![]() ,延长
,延长![]() 交
交![]() 于点
于点![]() .
.

(1)求证:![]() 为
为![]() 的切线;
的切线;
(2)求证:![]() ;
;
(3)若![]() ,且
,且![]() ,求
,求![]() 的半径.
的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y1=kx+b与反比例函数y2=![]() 的图象交于A(2,3),B(6,n)两点,与x轴、y轴分别交于C,D两点.
的图象交于A(2,3),B(6,n)两点,与x轴、y轴分别交于C,D两点.
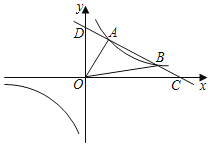
(1)求一次函数与反比例函数的解析式.
(2)求当x为何值时,y1>0.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有甲、乙两个不透明的布袋,甲袋中有两个完全相同的小球,分别标有数字1和-2;乙袋中有三个完全相同的小球,分别标有数字-1、0和2.小丽先从甲袋中随机取出一个小球,记录下小球上的数字为x;再从乙袋中随机取出一个小球,记录下小球上的数字为y,设点A的坐标为(x,y).
(1)请用表格或树状图列出点A所有可能的坐标;
(2)求点A在反比例函数y=![]() 图象上的概率.
图象上的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校3月份开展网络授课教学,该校随机抽取部分学生,按四个类别(A、很喜欢;B、喜欢;C、一般;D、不喜欢;)统计它们对网络授课的接受情况,并将结果绘制成如下两幅不完整的统计图:
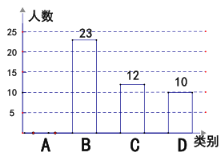
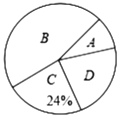
(1)这次共抽取_________名学生进行统计调查;扇形统计图中,D类所对应的扇形圆心角的大小为_______;
(2)将条形图补充完整;
(3)该校共有1500名学生,估计该校表示“喜欢”网络授课的B类的学生大约有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】上海世博会已于2010年4月30日开幕,各国游客都被吸引到了这个地方,据统计到5月10号为止最高单日接待量已达到100万人次,其中中国馆自然是最受欢迎的展馆,在世博会开园第一天共接待了游客3万余人,而外国场馆中最受欢迎的依次是瑞士馆、法国馆、德国馆、西班牙馆、日本馆.现将某天世博会最受欢迎的6个馆的参观人数用统计图①②分别表示如下:
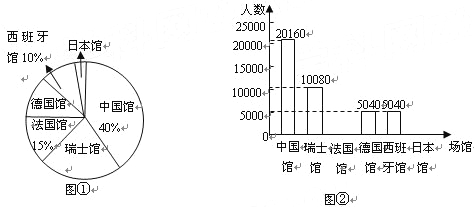
请根据统计图回答下列问题:
(1)这一天参观这6个场馆的总人数为 __ ,其中参观日本馆的人数有__,德国馆所在扇形的圆心角度数为__;
(2)请将条形统计图补充完整;
(3)小宝和小贝都想利用暑假去上海参观世博会,恰好张伯伯有一张世博会的门票,小宝和小贝都想得到这张门票.于是他们决定用转转盘的游戏来决定这张票由谁获得,游戏规则如下:将一质地均匀的转盘等分成5个面积相等的扇形,上面分别标有数字 -l,4,5,-6,0,小宝和小贝均随机地转转盘一次,把指针指向区域内的数字分别记为x、y.若指针指在边界,则重新转一次直到指针指向一个区域内为止,然后他们计算出xy的值.规定:当xy的值为负数时,门票归小宝;xy的值为正数时,门票归小贝.请利用表格或树状图游戏对双方公平吗?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某服装加工厂甲、乙两个车间共同加工一款休闲装,且每人每天加工的件数相同,甲车间比乙车间少10人,甲车间每天加工服装400件,乙车间每天加工服装600件.
(1)求甲、乙两车间各有多少人;
(2)甲车间更新了设备,平均每人每天加工的件数比原来多了10件,乙车间的加工效率不变,在两个车间总人数不变的情况下,加工厂计划从乙车间调出一部分人到甲车间,使每天两个车间加工的总数不少于1314件,求至少要从乙车间调出多少人到甲车间.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c(a≠0)的图象如图,则下列4个结论:①abc<0;②2a+b=0;③4a+2b+c>0;④b2﹣4ac>0;其中正确的结论的个数是( )
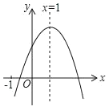
A.1B.2C.3D.4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com