
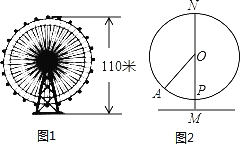
【题目】如图1,有一直径为100米的摩天轮,其最高点距离地面高度为110米,该摩天轮匀速转动(吊舱每分钟转过的角度相同)一周的时间为24分钟.
(1)如图2,某游客所在吊舱从最低点P出发,3分钟后到达A处,此时该游客离地面高度约为多少米;(精确到整数)
(2)该游客在摩天轮转动一周的过程中,有多少时间距离地面不低于85米?(参考数据:![]() ≈1.41,
≈1.41,![]() =1.73)
=1.73)
【答案】(1)15米;(2)8分
【解析】
(1)作AH⊥MN于H,求出吊舱每分钟转过的角度,得到∠AOH,根据余弦的定义计算,得到答案;
(2)求出OE的长度,根据正弦的定义求出∠OCE=30°,得到∠COD=120°,根据题意计算即可.
解:(1)如图2,作AH⊥MN于H,
吊舱每分钟转过的角度=![]() =15°,
=15°,
∴3分钟转过的角度为45°,
在Rt△OAH中,OH=OAcos∠AOH=50×![]() =25
=25![]() ,
,
∴HM=60﹣25![]() ≈25,
≈25,
答:该游客离地面高度约为25米;
(2)如图2,线段CD距离地面85米,
则OE=85﹣60=25,
在Rt△OEC中,∠OEC=90°,OE=25,OC=50,
∴∠OCE=30°,
∴∠COE=60°,
∴∠COD=120°,
∴距离地面不低于85米的时间为:![]() =8(分).
=8(分).



 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+c经过点B(4,0),C(0,﹣2),对称轴为直线x=1,与x轴的另一个交点为点A.

(1)求抛物线的解析式;
(2)点M从点A出发,沿AC向点C运动,速度为1个单位长度/秒,同时点N从点B出发,沿BA向点A运动,速度为2个单位长度/秒,当点M、N有一点到达终点时,运动停止,连接MN,设运动时间为t秒,当t为何值时,AMN的面积S最大,并求出S的最大值;
(3)点P在x轴上,点Q在抛物线上,是否存在点P、Q,使得以点P、Q、B、C为顶点的四边形是平行四边形,若存在,直接写出所有符合条件的点P坐标,若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解某中学学生课余生活情况,对喜爱看课外书、体育活动、看电视、社会实践四个方面的人数进行调查统计.现从该校随机抽取![]() 名学生作为样本,采用问卷调查的方法收集数据(参与问卷调查的每名学生只能选择其中一项).并根据调查得到的数据绘制成了如图所示的两幅不完整的统计图.由图中提供的信息,解答下列问题:
名学生作为样本,采用问卷调查的方法收集数据(参与问卷调查的每名学生只能选择其中一项).并根据调查得到的数据绘制成了如图所示的两幅不完整的统计图.由图中提供的信息,解答下列问题:
(1)求n的值;
(2)若该校学生共有1200人,试估计该校喜爱看电视的学生人数;
(3)若调查到喜爱体育活动的4名学生中有3名男生和1名女生,现从这4名学生中任意抽取2名学生,求恰好抽到2名男生的概率.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,⊙O的直径AB为10cm,弦BC为5cm,D、E分别是∠ACB的平分线与⊙O,AB的交点,P为AB延长线上一点,且PC=PE.

(1)求AC、AD的长;
(2)试判断直线PC与⊙O的位置关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有一块形状如图的五边形余料![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .要在这块余料中截取一块矩形材料,其中一边在
.要在这块余料中截取一块矩形材料,其中一边在![]() 上,并使所截矩形的面积尽可能大.
上,并使所截矩形的面积尽可能大.
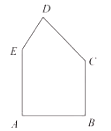
(1)若所截矩形材料的一条边是![]() 或
或![]() ,求矩形材料的面积;
,求矩形材料的面积;
(2)能否截出比(1)中面积更大的矩形材料?如果能,求出这些矩形材料面积的最大值,如果不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1和图2,在△ABC中,AB=13,BC=14,![]() .
.
探究:如图1,AH⊥BC于点H,则AH=___,AC=___,△ABC的面积![]() =___.
=___.
拓展:如图2,点D在AC上(可与点A、C重合),分别过点A、C作直线BD的垂线,垂足为E、F,设BD=x,AE=m,CF=n,(当点D与A重合时,我们认为![]() =0).
=0).
(1)用含x、m或n的代数式表示![]() 及
及![]() ;
;
(2)求(m+n)与x的函数关系式,并求(m+n)的最大值和最小值;
(3)对给定的一个x值,有时只能确定唯一的点D,指出这样的x的取值范围.
发现:请你确定一条直线,使得A、B、C三点到这条直线的距离之和最小(不必写出过程),并写出这个最小值.

查看答案和解析>>
科目:初中数学 来源: 题型:
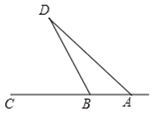
【题目】数学课外实践活动中,小李同学在河边的A,B两点处,利用测角仪分别对对岸的一观景亭D进行了测量.如图,测得∠DAC=45°,∠DBC=65°.若AB=132米,求观景亭D到AC的距离约为多少米?(结果精确到1米,参考数据:sin65°≈0.91,cos65°≈0.42,tan65°≈2.14)
查看答案和解析>>
科目:初中数学 来源: 题型:
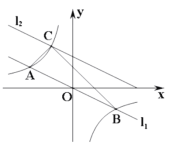
【题目】如图,在平面直角坐标系中,直线![]() 与反比例函数
与反比例函数![]() 的图象交于A,B两点(点A在点B左侧),已知A点的纵坐标是1:将直线
的图象交于A,B两点(点A在点B左侧),已知A点的纵坐标是1:将直线![]() 沿y向上平移后的直线
沿y向上平移后的直线![]() 与反比例函数
与反比例函数![]() 在第二象限内交于点C,如果
在第二象限内交于点C,如果![]() 的面积为3,则平移后的直线
的面积为3,则平移后的直线![]() 的函数表达式为_____.
的函数表达式为_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com