
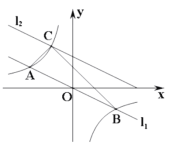
【题目】如图,在平面直角坐标系中,直线![]() 与反比例函数
与反比例函数![]() 的图象交于A,B两点(点A在点B左侧),已知A点的纵坐标是1:将直线
的图象交于A,B两点(点A在点B左侧),已知A点的纵坐标是1:将直线![]() 沿y向上平移后的直线
沿y向上平移后的直线![]() 与反比例函数
与反比例函数![]() 在第二象限内交于点C,如果
在第二象限内交于点C,如果![]() 的面积为3,则平移后的直线
的面积为3,则平移后的直线![]() 的函数表达式为_____.
的函数表达式为_____.
科目:初中数学 来源: 题型:
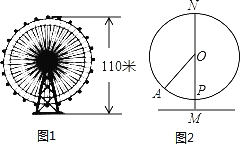
【题目】如图1,有一直径为100米的摩天轮,其最高点距离地面高度为110米,该摩天轮匀速转动(吊舱每分钟转过的角度相同)一周的时间为24分钟.
(1)如图2,某游客所在吊舱从最低点P出发,3分钟后到达A处,此时该游客离地面高度约为多少米;(精确到整数)
(2)该游客在摩天轮转动一周的过程中,有多少时间距离地面不低于85米?(参考数据:![]() ≈1.41,
≈1.41,![]() =1.73)
=1.73)
查看答案和解析>>
科目:初中数学 来源: 题型:
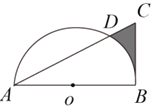
【题目】如图,在Rt△ABC中,∠ABC=90°,AB=![]() ,BC=2,以AB的中点为圆心,OA的长为半径作半圆交AC于点D,则图中阴影部分的面积为( )
,BC=2,以AB的中点为圆心,OA的长为半径作半圆交AC于点D,则图中阴影部分的面积为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
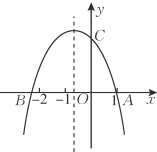
【题目】如图,抛物线y=![]() +bx+c(a≠0)与x轴交于点A(1,0)和B,与y轴的正半轴交于点C.下列结论:①abc>0;②4a-2b+c>0;③2a-b>0;④3a+c>0.其中正确结论的个数为( )
+bx+c(a≠0)与x轴交于点A(1,0)和B,与y轴的正半轴交于点C.下列结论:①abc>0;②4a-2b+c>0;③2a-b>0;④3a+c>0.其中正确结论的个数为( )
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】
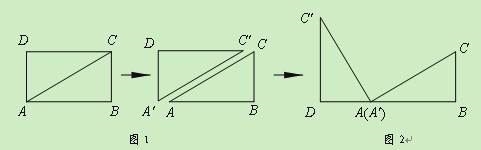
情境观察:将矩形ABCD纸片沿对角线AC剪开,得到△ABC和△A′C′D,如图1所示.将△A′C′D的顶点A′与点A重合,并绕点A按逆时针方向旋转,使点D、A(A′)、B在同一条直线上,如图2所示.
观察图2可知:与BC相等的线段是 ▲ ,∠CAC′= ▲ °.
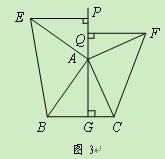
问题探究:如图3,△ABC中,AG⊥BC于点G,以A为直角顶点,分别以AB、AC为直角边,向△ABC外作等腰Rt△ABE和等腰Rt△ACF,过点E、F作射线GA的垂线,垂足分别为P、Q. 试探究EP与FQ之间的数量关系,并证明你的结论.
拓展延伸:如图4,△ABC中,AG⊥BC于点G,分别以AB、AC为一边向△ABC外作矩形ABME和矩形ACNF,射线GA交EF于点H. 若AB=k AE,AC=k AF,试探究HE与HF之间的数量关系,并说明理由.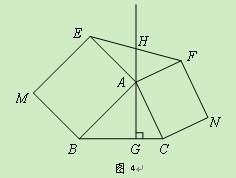
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 与x轴相交于A(3,0)、B两点,与y轴交于点C(0,3),点B在x轴的负半轴上,且
与x轴相交于A(3,0)、B两点,与y轴交于点C(0,3),点B在x轴的负半轴上,且![]() .
.

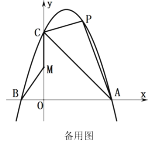
(1)求抛物线的函数关系式;
(2)若P是抛物线上且位于直线![]() 上方的一动点,求
上方的一动点,求![]() 的面积的最大值及此时点P的坐标;
的面积的最大值及此时点P的坐标;
(3)在线段![]() 上是否存在一点M,使
上是否存在一点M,使![]() 的值最小?若存在,请求出这个最小值及对应的M点的坐标;若不存在,请说明理由.
的值最小?若存在,请求出这个最小值及对应的M点的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,航模小组用无人机来测量建筑物BC的高度,无人机从A处测得建筑物顶部B的仰角为45°,测得底部C的俯角为60°,若此时无人机与该建筑物的水平距离AD为30m,则该建筑物的高度BC为_____m.(结果保留根号)
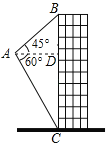
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】新型冠状病毒肺炎侵袭全国,全国人民团齐心协力共抗疫情.小明同学一直关注疫情的变化,期待疫情结束早日复课,他主要关注近一个月新增确诊病例和现有确诊病例的情况,如图1、图2所示,反映的是2020年2月22日至3月23日的新增确诊病例和现有确诊病例的情况.
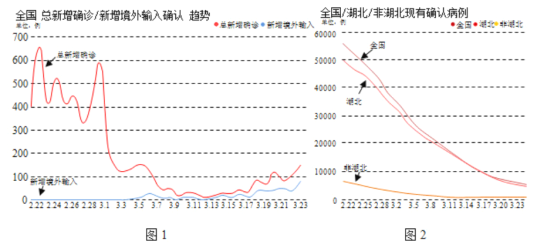
对2月22日至3月23日近一个月内数据,下面有四个推断
①全国新增境外输人确诊病例呈上升趋势;
②全国一天内新增确诊人数最多约650人;
③全国总新增确诊人数减少,全国现有确诊人数增加;
④全国一日新增确诊人数的中位数约为400.
其中合理推断的序号是( )
A.①②B.①④C.①②④D.①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
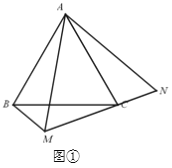
【题目】已知△ABC为等边三角形, M为三角形外任意一点,把△ABM绕着点A按逆时针方向旋转60°到△CAN的位置.
(1)如图①,若∠BMC=120°,BM=2,MC=3.求∠AMB的度数和求AM的长.
(2)如图②,若∠BMC = n°,试写出AM、BM、CM之间的数量关系,并证明你的猜想.
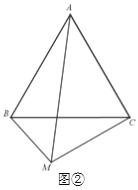
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com