
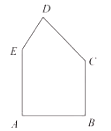
【题目】有一块形状如图的五边形余料![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .要在这块余料中截取一块矩形材料,其中一边在
.要在这块余料中截取一块矩形材料,其中一边在![]() 上,并使所截矩形的面积尽可能大.
上,并使所截矩形的面积尽可能大.
(1)若所截矩形材料的一条边是![]() 或
或![]() ,求矩形材料的面积;
,求矩形材料的面积;
(2)能否截出比(1)中面积更大的矩形材料?如果能,求出这些矩形材料面积的最大值,如果不能,请说明理由.
【答案】(1)S=30;(2)能,![]() 的最大值为30.25.
的最大值为30.25.
【解析】
(1)①若所截矩形材料的一条边是BC,过点C作CF⊥AE于F,得出S1=ABBC=6×5=30;
②若所截矩形材料的一条边是AE,过点E作EF∥AB交CD于F,FG⊥AB于G,过点C作CH⊥FG于H,则四边形AEFG为矩形,四边形BCHG为矩形,证出△CHF为等腰三角形,得出AE=FG=6,HG=BC=5,BG=CH=FH,求出BG=CH=FH=FG-HG=1,AG=AB-BG=5,得出S2=AEAG=6×5=30;
(2)在CD上取点F,过点F作FM⊥AB于M,FN⊥AE于N,过点C作CG⊥FM于G,则四边形ANFM为矩形,四边形BCGM为矩形,证出△CGF为等腰三角形,得出MG=BC=5,BM=CG,FG=DG,设AM=x,则BM=6-x,FM=GM+FG=GM+CG=BC+BM=11-x,得出S=AM×FM=x(11-x)=-x2+11x,由二次函数的性质即可得出结果.
(1)①若所截矩形材料的一条边是BC,如图1所示:
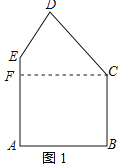
过点C作CF⊥AE于F,S1=ABBC=6×5=30;
②若所截矩形材料的一条边是AE,如图2所示:
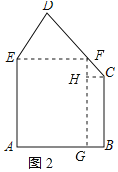
过点E作EF∥AB交CD于F,FG⊥AB于G,过点C作CH⊥FG于H,
则四边形AEFG为矩形,四边形BCHG为矩形,
∵∠C=135°,
∴∠FCH=45°,
∴△CHF为等腰直角三角形,
∴AE=FG=6,HG=BC=5,BG=CH=FH,
∴BG=CH=FH=FG-HG=6-5=1,
∴AG=AB-BG=6-1=5,
∴S2=AEAG=6×5=30;
(2)能;理由如下:
在CD上取点F,过点F作FM⊥AB于M,FN⊥AE于N,过点C作CG⊥FM于G,
则四边形ANFM为矩形,四边形BCGM为矩形,
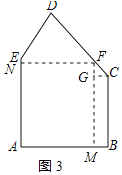
∵∠C=135°,
∴∠FCG=45°,
∴△CGF为等腰直角三角形,
∴MG=BC=5,BM=CG,FG=DG,
设AM=x,则BM=6-x,
∴FM=GM+FG=GM+CG=BC+BM=11-x,
∴S=AM×FM=x(11-x)=-x2+11x=-(x-5.5)2+30.25,
∴当x=5.5时,S的最大值为30.25.


科目:初中数学 来源: 题型:
【题目】操作发现:如图,已知△ABC和△ADE均为等腰三角形,AB=AC,AD=AE,将这两个三角形放置在一起,使点B,D,E在同一直线上,连接CE.

(1)如图1,若∠ABC=∠ACB=∠ADE=∠AED=55°,求证:△BAD≌△CAE;
(2)在(1)的条件下,求∠BEC的度数;
拓广探索:(3)如图2,若∠CAB=∠EAD=120°,BD=4,CF为△BCE中BE边上的高,请直接写出EF的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知四边形ABCD是矩形,把矩形沿直线AC折叠,点B落在点E处,
(1)求证:△AOE≌△COD;
(2)连接DE,若DE:AC=3:5,求tan∠ACB.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx﹣3a经过点A(﹣1,0)、C(0,3),与x轴交于另一点B,抛物线的顶点为D.
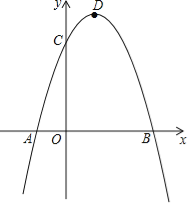
(1)求此二次函数解析式;
(2)连接DC、BC、DB,求证:△BCD是直角三角形;
(3)在对称轴右侧的抛物线上是否存在点P,使得△PDC为等腰三角形?若存在,求出符合条件的点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
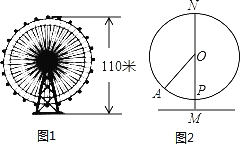
【题目】如图1,有一直径为100米的摩天轮,其最高点距离地面高度为110米,该摩天轮匀速转动(吊舱每分钟转过的角度相同)一周的时间为24分钟.
(1)如图2,某游客所在吊舱从最低点P出发,3分钟后到达A处,此时该游客离地面高度约为多少米;(精确到整数)
(2)该游客在摩天轮转动一周的过程中,有多少时间距离地面不低于85米?(参考数据:![]() ≈1.41,
≈1.41,![]() =1.73)
=1.73)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】端午节当天,小明带了四个粽子(除味道不同外,其它均相同),其中两个是大枣味的,另外两个是火腿味的,准备按数量平均分给小红和小刚两个好朋友.
(1)请你用树状图或列表的方法表示小红拿到的两个粽子的所有可能性;
(2)请你计算小红拿到的两个粽子刚好是同一味道的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系![]() 中,点
中,点![]() ,
,![]() ,
,![]() ,…和
,…和![]() ,
,![]() ,
,![]() ,…分别在直线
,…分别在直线![]() 和
和![]() 轴上.△OA1B1,△B1A2B2,△B2A3B3,…都是等腰直角三角形,如果
轴上.△OA1B1,△B1A2B2,△B2A3B3,…都是等腰直角三角形,如果![]() (1,1),
(1,1),![]() (
(![]() ),那么点
),那么点![]() 的纵坐标是_______.
的纵坐标是_______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】
情境观察:将矩形ABCD纸片沿对角线AC剪开,得到△ABC和△A′C′D,如图1所示.将△A′C′D的顶点A′与点A重合,并绕点A按逆时针方向旋转,使点D、A(A′)、B在同一条直线上,如图2所示.
观察图2可知:与BC相等的线段是 ▲ ,∠CAC′= ▲ °.
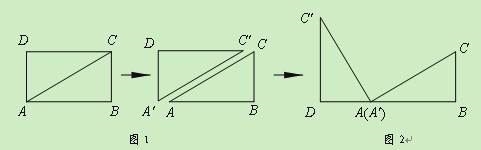
问题探究:如图3,△ABC中,AG⊥BC于点G,以A为直角顶点,分别以AB、AC为直角边,向△ABC外作等腰Rt△ABE和等腰Rt△ACF,过点E、F作射线GA的垂线,垂足分别为P、Q. 试探究EP与FQ之间的数量关系,并证明你的结论.
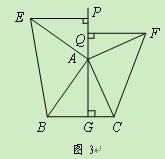
拓展延伸:如图4,△ABC中,AG⊥BC于点G,分别以AB、AC为一边向△ABC外作矩形ABME和矩形ACNF,射线GA交EF于点H. 若AB=k AE,AC=k AF,试探究HE与HF之间的数量关系,并说明理由.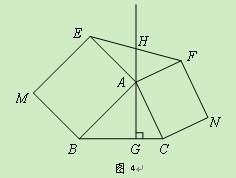
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com