
【题目】如图,已知四边形ABCD是矩形,把矩形沿直线AC折叠,点B落在点E处,
(1)求证:△AOE≌△COD;
(2)连接DE,若DE:AC=3:5,求tan∠ACB.

【答案】(1)见解析;(2)![]()
【解析】
(1)由矩形的性质和折叠的性质可得AE=CD,由“AAS”可证△AEO≌△CDO;
(2)由全等三角形的性质可得AO=CO,EO=DO,即可得![]() ,可证△DOE∽△COA,可得EO:CO=3:5,即可设EO=DO=3x,AO=CO=5x,AD=8x,由勾股定理可求CD=4x=AB,即可求解.
,可证△DOE∽△COA,可得EO:CO=3:5,即可设EO=DO=3x,AO=CO=5x,AD=8x,由勾股定理可求CD=4x=AB,即可求解.
解:证明:(1)∵四边形ABCD是矩形
∴AB=CD,AD=BC,∠B=∠ADC=90°,
∵折叠
∴AE=AB,
∵AE=CD,∠AOE=∠COD,∠AEC=∠ADC
∴△AEO≌△CDO(AAS)
(2)∵△AEO≌△CDO
∴AO=CO,EO=DO
∴![]() 且∠AOC=∠DOE
且∠AOC=∠DOE
∴△DOE∽△COA
∴![]() ,且DE:AC=3:5,
,且DE:AC=3:5,
∴EO:CO=3:5
设EO=DO=3x,AO=CO=5x,
∴DA=BC=8x,CD=![]() =4x=AB
=4x=AB
∴tan∠ACB=![]() =
=![]() =
=![]()


 备战中考寒假系列答案
备战中考寒假系列答案科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,BE、DF分别是平行四边形的两个外角的平分线,∠EAF=![]() ∠BAD,边AE、AF分别交两条角平分线于点E、F.
∠BAD,边AE、AF分别交两条角平分线于点E、F.
(1)求证:△ABE∽△FDA;
(2)联结BD、EF,如果DF2=ADAB,求证:BD=EF.

查看答案和解析>>
科目:初中数学 来源: 题型:
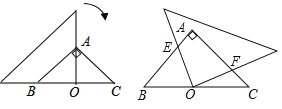
【题目】如图,在等腰直角三角形![]() 中,
中,![]() ,一个三角尺的直角顶点与
,一个三角尺的直角顶点与![]() 边的中点
边的中点![]() 重合,且两条直角边分别经过点
重合,且两条直角边分别经过点![]() 和点
和点![]() ,将三角尺绕点
,将三角尺绕点![]() 按顺时针方向旋转任意一个锐角,当三角尺的两直角边与
按顺时针方向旋转任意一个锐角,当三角尺的两直角边与![]() ,
,![]() 分别交于点
分别交于点![]() ,
,![]() 时,下列结论中错误的是( )
时,下列结论中错误的是( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解某中学学生课余生活情况,对喜爱看课外书、体育活动、看电视、社会实践四个方面的人数进行调查统计.现从该校随机抽取![]() 名学生作为样本,采用问卷调查的方法收集数据(参与问卷调查的每名学生只能选择其中一项).并根据调查得到的数据绘制成了如图所示的两幅不完整的统计图.由图中提供的信息,解答下列问题:
名学生作为样本,采用问卷调查的方法收集数据(参与问卷调查的每名学生只能选择其中一项).并根据调查得到的数据绘制成了如图所示的两幅不完整的统计图.由图中提供的信息,解答下列问题:
(1)求n的值;
(2)若该校学生共有1200人,试估计该校喜爱看电视的学生人数;
(3)若调查到喜爱体育活动的4名学生中有3名男生和1名女生,现从这4名学生中任意抽取2名学生,求恰好抽到2名男生的概率.

查看答案和解析>>
科目:初中数学 来源: 题型:
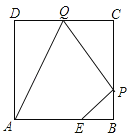
【题目】如图,已知正方形ABCD边长为3,点E在AB边上且BE=1,点P,Q分别是边BC,CD的动点(均不与顶点重合),当四边形AEPQ的周长取最小值时,四边形AEPQ的面积是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,⊙O的直径AB为10cm,弦BC为5cm,D、E分别是∠ACB的平分线与⊙O,AB的交点,P为AB延长线上一点,且PC=PE.

(1)求AC、AD的长;
(2)试判断直线PC与⊙O的位置关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
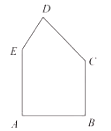
【题目】有一块形状如图的五边形余料![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .要在这块余料中截取一块矩形材料,其中一边在
.要在这块余料中截取一块矩形材料,其中一边在![]() 上,并使所截矩形的面积尽可能大.
上,并使所截矩形的面积尽可能大.
(1)若所截矩形材料的一条边是![]() 或
或![]() ,求矩形材料的面积;
,求矩形材料的面积;
(2)能否截出比(1)中面积更大的矩形材料?如果能,求出这些矩形材料面积的最大值,如果不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1和图2,在△ABC中,AB=13,BC=14,![]() .
.
探究:如图1,AH⊥BC于点H,则AH=___,AC=___,△ABC的面积![]() =___.
=___.
拓展:如图2,点D在AC上(可与点A、C重合),分别过点A、C作直线BD的垂线,垂足为E、F,设BD=x,AE=m,CF=n,(当点D与A重合时,我们认为![]() =0).
=0).
(1)用含x、m或n的代数式表示![]() 及
及![]() ;
;
(2)求(m+n)与x的函数关系式,并求(m+n)的最大值和最小值;
(3)对给定的一个x值,有时只能确定唯一的点D,指出这样的x的取值范围.
发现:请你确定一条直线,使得A、B、C三点到这条直线的距离之和最小(不必写出过程),并写出这个最小值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“五一劳动节大酬宾!”,某商场设计的促销活动如下:在一个不透明的箱子里放有4个相同的小球,球上分别标有“0元”、“10元”、“20元”和“50元”的字样.规定:在本商场同一日内,顾客每消费满300元,就可以在箱子里先后摸出两个球(第一次摸出后不放回).商场根据两小球所标金额的和返还相等价格的购物券,购物券可以在本商场消费.某顾客刚好消费300元.
(1)该顾客至多可得到________元购物券;
(2)请你用画树状图或列表的方法,求出该顾客所获得购物券的金额不低于50元的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com