
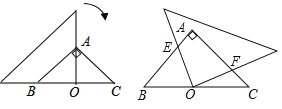
【题目】如图,在等腰直角三角形![]() 中,
中,![]() ,一个三角尺的直角顶点与
,一个三角尺的直角顶点与![]() 边的中点
边的中点![]() 重合,且两条直角边分别经过点
重合,且两条直角边分别经过点![]() 和点
和点![]() ,将三角尺绕点
,将三角尺绕点![]() 按顺时针方向旋转任意一个锐角,当三角尺的两直角边与
按顺时针方向旋转任意一个锐角,当三角尺的两直角边与![]() ,
,![]() 分别交于点
分别交于点![]() ,
,![]() 时,下列结论中错误的是( )
时,下列结论中错误的是( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
【答案】C
【解析】
连接AO,易证△EOA≌△FOC(ASA),利用全等三角形的性质可得出EA=FC,进而可得出AE+AF=AC,选项A正确;由三角形内角和定理结合∠B+∠C=90°,∠EOB+∠FOC=90°可得出∠BEO+∠OFC=180°,选项B正确;由△EOA≌△FOC可得出S△EOA=S△FOC,结合图形可得出S四边形AEOF=S△EOA+S△AOF=S△FOC+S△AOF=S△AOC=![]() S△ABC,选项D正确.综上,此题得解.
S△ABC,选项D正确.综上,此题得解.
连接AO,如图所示.
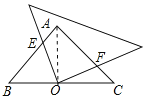
∵△ABC为等腰直角三角形,点O为BC的中点,
∴OA=OC,∠AOC=90°,∠BAO=∠ACO=45°.
∵∠EOA+∠AOF=∠EOF=90°,∠AOF+∠FOC=∠AOC=90°,
∴∠EOA=∠FOC.
在△EOA和△FOC中,
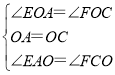 ,
,
∴△EOA≌△FOC(ASA),
∴EA=FC,
∴AE+AF=AF+FC=AC,选项A正确;
∵∠B+∠BEO+∠EOB=∠FOC+∠C+∠OFC=180°,∠B+∠C=90°,∠EOB+∠FOC=180°-∠EOF=90°,
∴∠BEO+∠OFC=180°,选项B正确;
∵△EOA≌△FOC,
∴S△EOA=S△FOC,
∴S四边形AEOF=S△EOA+S△AOF=S△FOC+S△AOF=S△AOC=![]() S△ABC,选项D正确.
S△ABC,选项D正确.
故选C.


 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案科目:初中数学 来源: 题型:
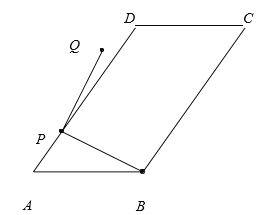
【题目】如图,在平行四边形ABCD中,AB=10,BC=15,tan∠A=![]() 点P为AD边上任意一点,连结PB,将PB绕点P逆时针旋转90°得到线段PQ.若点Q恰好落在平行四边形ABCD的边所在的直线上,则PB旋转到PQ所扫过的面积____(结果保留π)
点P为AD边上任意一点,连结PB,将PB绕点P逆时针旋转90°得到线段PQ.若点Q恰好落在平行四边形ABCD的边所在的直线上,则PB旋转到PQ所扫过的面积____(结果保留π)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,双曲线![]() 与直线
与直线![]() 相交于
相交于![]() ,点P是x轴上一动点.
,点P是x轴上一动点.
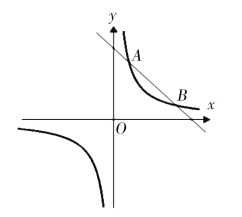
(1)求双曲线![]() 与直线
与直线![]() 的解析式;
的解析式;
(2)当![]() 时,直接写出x的取值范围;
时,直接写出x的取值范围;
(3)当![]() 是等腰三角形时,求点P的坐标.
是等腰三角形时,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,BC是⊙O的切线,D是⊙O上的一点,且AD//CO.

(1)求证:△ADB∽△OBC;
(2)若AB=2,BC=![]() ,求AD的长.(结果保留根号)
,求AD的长.(结果保留根号)
查看答案和解析>>
科目:初中数学 来源: 题型:
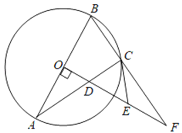
【题目】如图,△ABC内接于⊙O,AB为直径,作OD⊥AB交AC于点D,延长BC,OD交于点F,过点C作⊙O的切线CE,交OF于点E.
(1)求证:EC=ED;
(2)如果OA=4,EF=3,求弦AC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】操作发现:如图,已知△ABC和△ADE均为等腰三角形,AB=AC,AD=AE,将这两个三角形放置在一起,使点B,D,E在同一直线上,连接CE.

(1)如图1,若∠ABC=∠ACB=∠ADE=∠AED=55°,求证:△BAD≌△CAE;
(2)在(1)的条件下,求∠BEC的度数;
拓广探索:(3)如图2,若∠CAB=∠EAD=120°,BD=4,CF为△BCE中BE边上的高,请直接写出EF的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知四边形ABCD是矩形,把矩形沿直线AC折叠,点B落在点E处,
(1)求证:△AOE≌△COD;
(2)连接DE,若DE:AC=3:5,求tan∠ACB.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系![]() 中,点
中,点![]() ,
,![]() ,
,![]() ,…和
,…和![]() ,
,![]() ,
,![]() ,…分别在直线
,…分别在直线![]() 和
和![]() 轴上.△OA1B1,△B1A2B2,△B2A3B3,…都是等腰直角三角形,如果
轴上.△OA1B1,△B1A2B2,△B2A3B3,…都是等腰直角三角形,如果![]() (1,1),
(1,1),![]() (
(![]() ),那么点
),那么点![]() 的纵坐标是_______.
的纵坐标是_______.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com