
【题目】如图,在△ABC中,∠BAC=90°,AB=AC=2,以AB为直径的圆交BC于D,则图中阴影部分的面积为( )
A.1
B.2
C.1+ ![]()
D.2﹣ ![]()
【答案】A
【解析】解:连接AD,OD

∵∠BAC=90°,AB=AC=2
∴△ABC是等腰直角三角形
∵AB是圆的直径
∴∠ADB=90°
∴AD⊥BC
∴点D是BC的中点
∴OD是△ABC的中位线
∴∠DOA=90°
∴△ODA,△ADC都是等腰直角三角形
∴两个弓形的面积相等
∴阴影部分的面积=S△ADC= ![]() AD2=1.
AD2=1.
所以答案是:A.
【考点精析】利用等腰直角三角形和三角形中位线定理对题目进行判断即可得到答案,需要熟知等腰直角三角形是两条直角边相等的直角三角形;等腰直角三角形的两个底角相等且等于45°;连接三角形两边中点的线段叫做三角形的中位线;三角形中位线定理:三角形的中位线平行于三角形的第三边,且等于第三边的一半.


科目:初中数学 来源: 题型:
【题目】图①、图②是8×5的正方形网格,线段AB、BC的端点均在格点上.按要求在图①、图②中以AB、BC为邻边各画一个四边形ABCD,使点D在格点上.要求所画两个四边形不全等,且同时满足四边形ABCD是轴对称图形,点D到∠ABC两边的距离相等.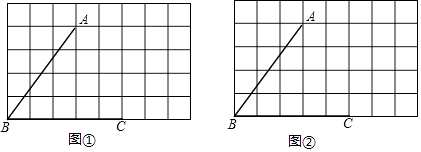
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校对七、八、九年级的学生进行体育水平测试,成绩评定为优秀、良好、合格、不合格四个等第.为了解这次测试情况,学校从三个年级随机抽取200名学生的体育成绩进行统计分析.相关数据的统计图、表如下:
各年级学生成绩统计表 | ||||
优秀 | 良好 | 合格 | 不合格 | |
七年级 | a | 20 | 24 | 8 |
八年级 | 29 | 13 | 13 | 5 |
九年级 | 24 | b | 14 | 7 |
根据以上信息解决下列问题:
(1)在统计表中,a的值为 , b的值为;
(2)在扇形统计图中,八年级所对应的扇形圆心角为度;
(3)若该校三个年级共有2000名学生参加考试,试估计该校学生体育成绩不合格的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xoy中,已知A(6,0),B(8,6),将线段OA平移至CB,点D在x轴正半轴上(不与点A重合),连接OC、AB、CD、BD.
(1)写出点C的坐标;
(2)当△ODC的面积是△ABD的面积的3倍时,求点D的坐标;
(3)设∠OCD=α,∠DBA=β,∠BDC=θ,判断α、β、θ之间的数量关系,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等边△ABC的边长为10cm,点D从点C出发沿CA向点A运动,点E从点B出发沿AB的延长线BF向右运动,已知点D,E都以1cm/s的速度同时开始运动,运动过程中DE与BC相交于点P,点D运动到点A后两点同时停止运动.
(1)当△ADE是直角三角形时,求D,E两点运动的时间;
(2)求证:在运动过程中,点P始终是线段DE的中点.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】![]() 与
与![]() 在平面直角坐标系中的位置如图
在平面直角坐标系中的位置如图

(1)分别写出下列各点的坐标:A′_____;B′______;C′_____.
(2)若点![]() 是
是![]() 内部一点,则平移后
内部一点,则平移后![]() 内的对应点
内的对应点![]() 的坐标为_______.
的坐标为_______.
(3)求![]() 的面积.
的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某村为了尽早摆脱贫穷落后的现状,积极响应国家号召,15位村民集资8万元,承包了一些土地种植有机蔬菜和水果,种这两种作物每公顷需要人数和投入资金如下表:
作物种类 | 每公顷所需人数/人 | 每公顷投入资金/万元 |
蔬菜 | 4 | 2 |
水果 | 5 | 3 |
在现有条件下,这15位村民应承包多少公顷土地,怎样安排能使每人都有事可做,并且资金正好够用?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在下列网格中建立平面直角坐标系如图,每个小正方形的边长均为1个单位长度.已知A(1,1)、B(3,4)和C(4,2).
(1)在图中标出点A、B、C.
(2)将点C向下平移3个单位到D点,将点A先向左平移3个单位,再向下平移1个单位到E点,在图中标出D点和E点.
(3)求△EBD的面积S△EBD.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】四边形ABCD中,∠A=140°,∠D=80°.

(1)如图1,若∠B=∠C,试求出∠C的度数;
(2)如图2,若∠ABC的角平分线BE交DC于点E,且BE∥AD,试求出∠C的度数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com