
【题目】如图,在平面直角坐标系xoy中,已知A(6,0),B(8,6),将线段OA平移至CB,点D在x轴正半轴上(不与点A重合),连接OC、AB、CD、BD.
(1)写出点C的坐标;
(2)当△ODC的面积是△ABD的面积的3倍时,求点D的坐标;
(3)设∠OCD=α,∠DBA=β,∠BDC=θ,判断α、β、θ之间的数量关系,并说明理由.

【答案】(1) C(2,6);(2) ![]() D(9,0)(3)α+β=θ或αβ=θ.
D(9,0)(3)α+β=θ或αβ=θ.
【解析】
(1)由点的坐标的特点,确定出FC=2,OF=6,得出C(2,6);
(2)分点D在线段OA和在OA延长线两种情况进行计算;
(3)分点D在线段OA上时,α+β=θ和在OA延长线α-β=θ两种情况进行计算;
(1)如图1,
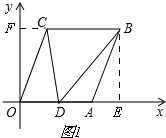
∵A(6,0),B(8,6),
∴FC=AE=86=2,OF=BE=6
∴C(2,6);
(2)设D(x,0),当△ODC的面积是△ABD的面积的3倍时,
若点D在线段OA上,
∵OD=3AD,
∴![]()
∴![]()
∴![]()
若点D在线段OA延长线上,
∵OD=3AD,
∴![]()
∴x=9,
∴D(9,0)
(3)如图2.

过点D作DE∥OC,
由平移的性质知OC∥AB.
∴OC∥AB∥DE.
∴∠OCD=∠CDE,∠EDB=∠DBA.
若点D在线段OA上,
∠CDB=∠CDE+∠EDB=∠OCD+∠DBA,
即α+β=θ;
若点D在线段OA延长线上,
∠CDB=∠CDE∠EDB=∠OCD∠DBA,
即αβ=θ.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】利用如图1的二维码可以进行身份识别.某校建立了一个身份识别系统,图2是某个学生的识别图案,黑色小正方形表示1,白色小正方形表示0.将第一行数字从左到右依次记为![]() ,
,![]() ,
,![]() ,
,![]() ,那么可以转换为该生所在班级序号,其序号为
,那么可以转换为该生所在班级序号,其序号为![]() .如图2第一行数字从左到右依次为0,1,0,1,序号为
.如图2第一行数字从左到右依次为0,1,0,1,序号为![]() ,表示该生为5班学生.表示6班学生的识别图案是( )
,表示该生为5班学生.表示6班学生的识别图案是( )


A.  B.
B.  C.
C.  D.
D. 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,BF平分∠ABC,AF⊥BF于点F,D为AB的中点,连接DF延长交AC于点E.若AB=10,BC=16,则线段EF的长为( )
A.2
B.3
C.4
D.5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,点P在线段AB外,且PA=PB,求证:点P在线段AB的垂直平分线上,在证明该结论时,需添加辅助线,则作法不正确的是( )
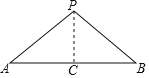
A. 作∠APB的平分线PC交AB于点C
B. 过点P作PC⊥AB于点C且AC=BC
C. 取AB中点C,连接PC
D. 过点P作PC⊥AB,垂足为C
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AM∥BN,∠A=80°,点P是射线AM上动点(与A不重合),BC、BD分别平分∠ABP和∠PBN,交射线AM于C、D.
(1)求∠CBD的度数;
(2)当点P运动时,那么∠APB:∠ADB的度数比值是否随之发生变化?若不变,请求出这个比值;若变化,请找出变化规律;
(3)当点P运动到使∠ACB=∠ABD时,求∠ABC的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,方格纸中每个小方格都是边长为1个单位长度的正方形,在建立平面直角坐标系后,△ABC的顶点在格点上.且A(1,﹣4),B(5,﹣4),C(4,﹣1)
(1)求出△ABC的面积;
(2)若把△ABC向上平移2个单位长度,再向左平移4个单位长度得到△A′B′C′,在图中画出△A′B′C′,并写出B′的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠BAC=90°,AB=AC=2,以AB为直径的圆交BC于D,则图中阴影部分的面积为( )
A.1
B.2
C.1+ ![]()
D.2﹣ ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算
(1)-2a2(![]() ab+b2)-5a(a2b-ab2)
ab+b2)-5a(a2b-ab2)
(2)计算9(x+2)(x-2)-(3x-2)2
(3)计算(a-b+c)(a-b-c)
(4)用乘法公式计算:![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,菱形ABCD中,AB=10,连接BD,tan∠ABD= ![]() ,若P是射线BC上的一个动点(点P不与点B重合),连接AP,与对角线相交于点E,连接EC.
,若P是射线BC上的一个动点(点P不与点B重合),连接AP,与对角线相交于点E,连接EC.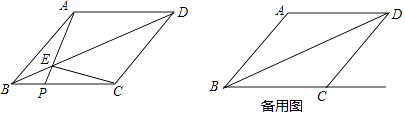
(1)求证:AE=CE;
(2)当点P在线段BC上时,设BP=x,S△EPC=y,求y关于x的函数解析式,并写出x的取值范围;
(3)当点P在线段BC的延长线上时,若△EPC是直角三角形,求线段BP的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com