
如图,在△ABC中,∠A=90°,AB=2cm,AC=4cm.动点P从点A出发,沿AB方向以1cm/s的速度向点B运动,动点Q从点B同时出发,沿BA方向以1cm/s的速度向点A运动.当点P到达点B时,P,Q两点同时停止运动,以AP为一边向上作正方形APDE,过点Q作Q F∥BC,交AC于点F.设点P的运动时间为ts,正方形和梯形重合部分的面积为Scm2.
F∥BC,交AC于点F.设点P的运动时间为ts,正方形和梯形重合部分的面积为Scm2.
(1)当t= _________ s时,点P与点Q重合;
(2)当t= _________ s时,点D在QF上;
(3)当点P在Q,B两点之间(不包括Q ,B两点)时,求S与t之间的函数关系式.
,B两点)时,求S与t之间的函数关系式.

(1)1 (2)
 (3)
(3)
【解析】
试题分析:(1)当点P与点Q重合时,AP=BQ=t,且AP+BQ=AB=2,
∴t+t=2,解得t=1s,
故填空答案:1.

(3)当P、Q重合时,由(1)知,此时t=1;
当D点在BC上时,如答图2所示,此时AP=BQ=t,BP= t,求得t=
t,求得t= s,进一步分析可知此时点E与点F重合;
s,进一步分析可知此时点E与点F重合;
当点P到达B点时,此时t=2.
因此当P点在Q,B两点之间(不包括Q,B两点)时,其运动过程可分析如下:
①当1<t≤ 时,如答图3所示,此时重合部分为梯形PDGQ.
时,如答图3所示,此时重合部分为梯形PDGQ.
此时AP=BQ=t,∴AQ=2﹣t,PQ=AP﹣AQ=2t﹣2;
易知△ABC∽△AQF,可得AF=2AQ,EF=2EG.
∴EF=AF﹣AE=2(2﹣t)﹣t=4﹣3t,EG= EF=2﹣
EF=2﹣ t,
t,
∴DG=DE﹣EG=t﹣(2﹣ t)=
t)= t﹣2.
t﹣2.
S=S梯形PDGQ= (PQ+DG)•PD=
(PQ+DG)•PD= [(2t﹣2)+(
[(2t﹣2)+( t﹣2)]•t=
t﹣2)]•t= t2﹣2t;
t2﹣2t;

综上所述,当点P在Q,B两点之间(不包括Q,B两点)时,S与t之间的函数关系式为:
S= .
.


考点:相似形综合题;勾股定理;正方形的性质;相似三角形的判定与性质.
点评:本题是运动型综合题,涉及到动点与动线问题.第(1)(2)问均涉及动点问题,列方程即可求出t的值;第(3)问涉及动线问题,是本题难点所在,首先要正确分 析动线运动过程,然后再正确计算其对应的面积S.本题难度较大,需要同学们具备良好的空间想象能力和较强的逻辑推理能力.
析动线运动过程,然后再正确计算其对应的面积S.本题难度较大,需要同学们具备良好的空间想象能力和较强的逻辑推理能力.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
已知抛物线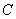
 :
:
 的顶点在坐标轴上.
的顶点在坐标轴上.
(1)求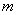
 的值;
的值;
(2)
 时,抛物线
时,抛物线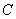
 向下平移
向下平移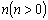
 个单位后与抛物线
个单位后与抛物线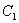
 :
: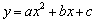
 关于
关于
 轴对称,且
轴对称,且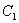
 过点
过点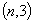
 ,求
,求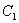
 的函数关系式;
的函数关系式;
(3)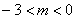
 时,抛物线
时,抛物线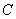
 的顶点为
的顶点为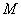
 ,且过点
,且过点
 .问在直线
.问在直线
 上是否存在一点
上是否存在一点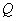
 使得△
使得△
 的周长最小,如果存在,求出点
的周长最小,如果存在,求出点
 的坐标, 如果不存在,请说明理由.
的坐标, 如果不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,在Rt△ABC中,∠C=90°,∠A=45°,AB=2.将△ABC绕顶点A顺时针方向旋转至△ AB′C′的位置,B,A,C′三点共线,则线段BC扫过的区域面积为 .
AB′C′的位置,B,A,C′三点共线,则线段BC扫过的区域面积为 .

查看答案和解析>>
科目:初中数学 来源: 题型:
在平面直角坐标系xOy中,一次函数y= 2x+2的图象与x轴交于A,与y轴交于点C,点B的坐标为(a,0),(其中a>0),直线l过动点M(0,m)(0<m<2),且与x轴平行,并与直线AC、BC分别相交于点D、E,P点在y轴上(P点异于C点)满足PE=
2x+2的图象与x轴交于A,与y轴交于点C,点B的坐标为(a,0),(其中a>0),直线l过动点M(0,m)(0<m<2),且与x轴平行,并与直线AC、BC分别相交于点D、E,P点在y轴上(P点异于C点)满足PE= CE,直线PD与x轴交于点Q,连接PA.
CE,直线PD与x轴交于点Q,连接PA.
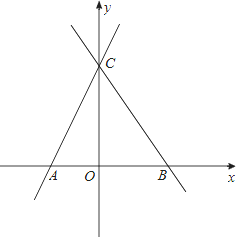
(1)写出A、C两点的坐标;
(2)当0<m<1时,若△PAQ是以P为顶点的倍边三角形(注:若△HNK满足HN=2HK,则称△HNK为以H为顶点的倍边三角形),求出m的值;
(3)当1<m<2时,是否存在实数m,使CD•AQ=PQ•DE?若能,求出m的值(用含a的代数式表示);若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,已知抛物线y=ax2+bx(a≠0)经过A(3,0)、B(4,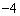 )两点。
)两点。
(1)求抛物线的解析式;
(2)将抛物线向下平移m个单位长度后,得到的抛物线与直线OB只有两个公共点D,求m的取值范围。

查看答案和解析>>
科目:初中数学 来源: 题型:
如图,抛物线y=﹣(x﹣1)2+c与x轴交于A,B(A,B分别 在y轴的左右两侧)两点,与y轴的正半轴交于点C,顶点为D,已知A(﹣1,0).
在y轴的左右两侧)两点,与y轴的正半轴交于点C,顶点为D,已知A(﹣1,0).

(1)求点B,C的坐标;
(2)判断△CDB的形状并说明理由;
(3)将△COB沿x轴向右平移t个单位长度(0<t<3)得到△QPE.△QPE与△CDB重叠部分(如图中阴影部分)面积为S,求S与t的函数关系式,并写出自变量t的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,在Rt△ABC中,∠ACB=90°,AC= 8cm,BC=4cm,D、E分别为边AB、BC的中点
8cm,BC=4cm,D、E分别为边AB、BC的中点 ,连结DE,点P从点A出发,沿折线AD-DE-EB运动,到点B停止.点P在AD上以
,连结DE,点P从点A出发,沿折线AD-DE-EB运动,到点B停止.点P在AD上以
 cm/s的速度运动,在折线DE-EB上以1cm/s的速度运动.当点P与点A不重合时,过点P作PQ⊥AC于点Q,以PQ为边作正方形PQMN,使点M落在线段AC上.设点P的运动时间为t(s).
cm/s的速度运动,在折线DE-EB上以1cm/s的速度运动.当点P与点A不重合时,过点P作PQ⊥AC于点Q,以PQ为边作正方形PQMN,使点M落在线段AC上.设点P的运动时间为t(s).
(1)当点P在线段DE上运动时,线段DP的 长为______cm,(用含t的代数式表示).
长为______cm,(用含t的代数式表示).
(2)当点N落在AB边上时,求t的值.
(3)当正方形PQMN与△ABC重叠部分图形为 五边形时,设五边形的面积为S(cm²),求S与t的函数关系式.
五边形时,设五边形的面积为S(cm²),求S与t的函数关系式.
(4)连结CD.当点N于点D重合时,有一点H从点M出 发,在线段MN上以2.5cm/s的速
发,在线段MN上以2.5cm/s的速 度沿M-N-M连续做往返运动,直至点P与点E重合时,点H停止往返运动;当点P在线段EB上运动时,点H始终在线段MN的中心处.直接写出在点P的整个运动过程中,点H落在线段CD上时t的取值范围.
度沿M-N-M连续做往返运动,直至点P与点E重合时,点H停止往返运动;当点P在线段EB上运动时,点H始终在线段MN的中心处.直接写出在点P的整个运动过程中,点H落在线段CD上时t的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,O为坐标原点,点B在x轴的正半轴上,四边形OACB是平行四边形,反比例函数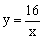 在第一象限内的图象经过点A,与
在第一象限内的图象经过点A,与 BC交于点F,OB=
BC交于点F,OB=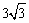 ,BF=
,BF=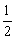 BC。过
BC。过 点F作EF∥OB,交OA于点,点
点F作EF∥OB,交OA于点,点 P为
P为 直线EF上的一个动点,连接PA,PO。若以P、O、A为顶点的三角形是直角三角形,请求出所有点P的坐标。
直线EF上的一个动点,连接PA,PO。若以P、O、A为顶点的三角形是直角三角形,请求出所有点P的坐标。

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com