
已知抛物线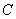
 :
:
 的顶点在坐标轴上.
的顶点在坐标轴上.
(1)求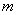
 的值;
的值;
(2)
 时,抛物线
时,抛物线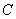
 向下平移
向下平移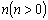
 个单位后与抛物线
个单位后与抛物线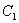
 :
: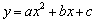
 关于
关于
 轴对称,且
轴对称,且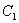
 过点
过点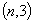
 ,求
,求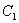
 的函数关系式;
的函数关系式;
(3)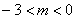
 时,抛物线
时,抛物线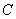
 的顶点为
的顶点为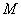
 ,且过点
,且过点
 .问在直线
.问在直线
 上是否存在一点
上是否存在一点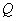
 使得△
使得△
 的周长最小,如果存在,求出点
的周长最小,如果存在,求出点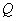
 的坐标, 如果不存在,请说明理由.
的坐标, 如果不存在,请说明理由.
 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南大学出版社系列答案
同步练习西南大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案科目:初中数学 来源: 题型:
如图,一大桥有一段抛物线型的拱梁,抛物线的表达式为y=ax2+bx+c,小王骑自行车从O匀速沿直线到拱梁一端A,再匀速通过拱梁部分的桥面AC,小王从O到A用了2秒, 当小王骑自行车行驶10秒时和20秒时拱梁的高度相同,则小强骑自行车通过拱梁部分的桥面AC共需
当小王骑自行车行驶10秒时和20秒时拱梁的高度相同,则小强骑自行车通过拱梁部分的桥面AC共需  秒.
秒.


查看答案和解析>>
科目:初中数学 来源: 题型:
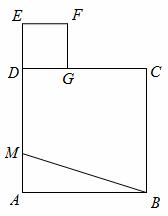
如图,在边长为3的正方形ABCD中,点M在边AD上,且AM=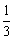 AD,延长M
AD,延长M D至点E,使ME=MB,以DE为边作正方形DEFG,点G在边CD上,则
D至点E,使ME=MB,以DE为边作正方形DEFG,点G在边CD上,则 DG 的长为 。
DG 的长为 。
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,△ABC中,已知∠BAC=45°,AD⊥BC于D,BD=2,DC=3,求AD 的长。
的长。
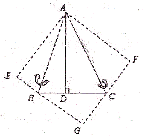

小萍同学灵活运用了轴对称知识,将图形进行翻折变换,巧妙地解答了此题。
(1)分别以AB、AC为对称轴,画出△ABD、△ACD的轴对称图形,D、C点的对称点分别为E、F,延长EB、FC相交于G点,求证:四边形AEGF是正方形;
(2)设AD=x,利用勾股定理,建立关于x的方程模型,求出x的值。
查看答案和解析>>
科目:初中数学 来源: 题型:
定义:如果一个y与x的函 数图象经过平移后能与某反比例函数的图象重合,那么称这个函数是y与x的“反比例平移函数”.例如:
数图象经过平移后能与某反比例函数的图象重合,那么称这个函数是y与x的“反比例平移函数”.例如: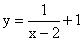
 的图象向左平移2个单位,再向下平移1个单位得到
的图象向左平移2个单位,再向下平移1个单位得到
 的图象,则
的图象,则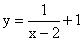
 是y与x的“反比例平移函数”.
是y与x的“反比例平移函数”.
(1)若矩形的两边分别是2cm、3cm,当这两边分别增加x(cm)、y(cm)后,得到的新矩形的面积为8cm2,求y与x的函数表达式,并判断这个函数是否为“反比例平移函数”.
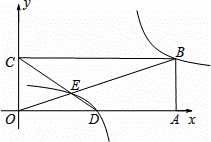
(2)如图,在平面直角坐标系中,点O为原点,矩形OABC的顶点A、C的坐标分别为(9,0)、(0,3).点D是OA的中点,连接OB、CD交于点E,“反比例平移函数”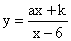
 的图象经过B、E两点.则这
的图象经过B、E两点.则这 个“反比例平移
个“反比例平移 函数”的表达式为 ;这个“反比例平移函数”的图象经过适当的变换与某一个反比例函数的图象重合,请写出这个反比例函数的表达式.
函数”的表达式为 ;这个“反比例平移函数”的图象经过适当的变换与某一个反比例函数的图象重合,请写出这个反比例函数的表达式.
(3)在(2)的条件下,已知过线段BE中点的一条直线l交这个“反比例平移函数”图象于P、Q两点(P在Q的右侧),若B、E、P、Q为顶点组成的四边形面积为16,请求出点P的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
如图所示,半径为1的圆和边长为1的正方形在同一水平线上,圆沿该水平线从左向右匀速穿过正方形,设穿过时间为t,正方形除去圆部分的面积为S(阴影部分),则S与t的大致图象为【 】

A. B.
B. C.
C. 8 D.
8 D.
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,在△ABC中,∠A=90°,AB=2cm,AC=4cm.动点P从点A出发,沿AB方向以1cm/s的速度向点B运动,动点Q从点B同时出发,沿BA方向以1cm/s的速度向点A运动.当点P到达点B时,P,Q两点同时停止运动,以AP为一边向上作正方形APDE,过点Q作Q F∥BC,交AC于点F.设点P的运动时间为ts,正方形和梯形重合部分的面积为Scm2.
F∥BC,交AC于点F.设点P的运动时间为ts,正方形和梯形重合部分的面积为Scm2.
(1)当t= _________ s时,点P与点Q重合;
(2)当t= _________ s时,点D在QF上;
(3)当点P在Q,B两点之间(不包括Q ,B两点)时,求S与t之间的函数关系式.
,B两点)时,求S与t之间的函数关系式.

查看答案和解析>>
科目:初中数学 来源: 题型:
如图1,在□ABC D中,AH⊥DC,垂足为H,AB=
D中,AH⊥DC,垂足为H,AB=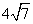 ,AD=7,AH=
,AD=7,AH=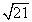 . 现有两个动点
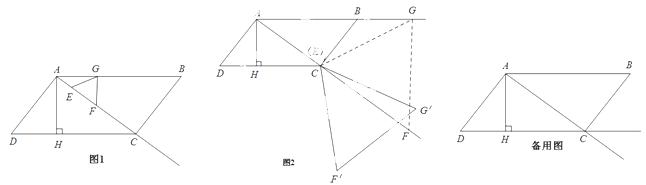
. 现有两个动点 E、F同时从点A出发,分别以每秒1个单位长度、每秒3个单位长度的速度沿射线AC方向匀速运动. 在点E、F运动过程中,以EF为边作等边△EFG,使△EFG与△ABC在射线AC的同侧,当点E运
E、F同时从点A出发,分别以每秒1个单位长度、每秒3个单位长度的速度沿射线AC方向匀速运动. 在点E、F运动过程中,以EF为边作等边△EFG,使△EFG与△ABC在射线AC的同侧,当点E运 动到点C时,E、F两点同时停止运动. 设运转时间为t秒.
动到点C时,E、F两点同时停止运动. 设运转时间为t秒.
(1)求线段AC的长;
(2)在整个运动过程中,设等边△EFG与△ABC重叠部分 的面积为S,请直接写出S与t之间的函数关系式
的面积为S,请直接写出S与t之间的函数关系式 ,并写出相应的自变量t的取值范围;
,并写出相应的自变量t的取值范围;
(3)当等边△EFG的顶点E到达点C时,如图2,将△EFG绕着点C旋转一个角度 . 在旋转过程中,点E与点C重合,F的对应点为F′,G的对应点为G′. 设直线F′G′与射线DC、射
. 在旋转过程中,点E与点C重合,F的对应点为F′,G的对应点为G′. 设直线F′G′与射线DC、射 线AC分别相交于M、N两点.试问:是否存在点M、N,使得△CMN是以∠MCN为底角的等腰三角形?若存在,请求出线段CM的长度;若不存在,请说明理由.
线AC分别相交于M、N两点.试问:是否存在点M、N,使得△CMN是以∠MCN为底角的等腰三角形?若存在,请求出线段CM的长度;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com