
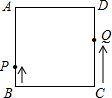
 ��֪������ABCD�У�AB=BC=CD=AD=10cm������P��Q�ֱ�ӵ�B��Cͬʱ�����������ε������˶������P���˶��ٶ�Ϊ2cm/s����Q���˶��ٶ�Ϊ3cm/s�����P��Q�˶���ʱ��Ϊt��s��
��֪������ABCD�У�AB=BC=CD=AD=10cm������P��Q�ֱ�ӵ�B��Cͬʱ�����������ε������˶������P���˶��ٶ�Ϊ2cm/s����Q���˶��ٶ�Ϊ3cm/s�����P��Q�˶���ʱ��Ϊt��s������ ��1�����P��Q�˶���ʱ��Ϊt�����������г����̽�ɣ�
��2�����P��Q�˶���ʱ��Ϊt�����������г����̽�ɣ�
��3�����P��Q�˶���ʱ��Ϊt������������г����̽��
��� �⣺��1����2+3��t=10��3�����t=6��
��2����2+3��t=10��3+10��4��99�����t=798
798��2�£�10��4��=39��36��
����P��100������ʱ������39Ȧ��36�ף���������BC���ϣ�
��3����ͬΪ˳ʱ�뷽��ʱ����3-2��t=10�����t=10��
��ͬΪ��ʱֵ����ʱ����3-2��t=10��3�����t=30��
���� ���⿼��һԪһ�η��̵�Ӧ�ã��ؼ��Ǹ����ٶȡ�ʱ����·�̵Ĺ�ϵ�г����̽��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
 ��ͼ����ABC�У�AB��BC��BE��AC����1=��2��AD=AB�������н��۲���ȷ���ǣ�������
��ͼ����ABC�У�AB��BC��BE��AC����1=��2��AD=AB�������н��۲���ȷ���ǣ�������| A�� | BF=DF | B�� | ��1=��EFD | C�� | BF��EF | D�� | FD��BC |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� |  | B�� |  | C�� |  | D�� |  |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ������ABCD�У�AB=8��AD=6����M�ǶԽ���AC�ϵ�һ�����㣬��M��ΪԲ�ģ��߶�AM��Ϊ�뾶��һ����M������M����CΪ�˵�ľ���ABCD���Ͻصõ��߶�EF=$\frac{6}{5}$AM�����߶�AM�ij���$\frac{30}{7}$��5��
��ͼ������ABCD�У�AB=8��AD=6����M�ǶԽ���AC�ϵ�һ�����㣬��M��ΪԲ�ģ��߶�AM��Ϊ�뾶��һ����M������M����CΪ�˵�ľ���ABCD���Ͻصõ��߶�EF=$\frac{6}{5}$AM�����߶�AM�ij���$\frac{30}{7}$��5���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ��AB�ǡ�O���ң�CD�ǡ�O��ֱ����CD��AB������ΪE��AB=4��CE=1�����O�뾶����
��ͼ��AB�ǡ�O���ң�CD�ǡ�O��ֱ����CD��AB������ΪE��AB=4��CE=1�����O�뾶�����鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ��ʾ�����Եó�����ʽ��$\left\{\begin{array}{l}{ax+b��0}\\{cx+d��0}\end{array}\right.$�Ľ⼯��x��-1��
��ͼ��ʾ�����Եó�����ʽ��$\left\{\begin{array}{l}{ax+b��0}\\{cx+d��0}\end{array}\right.$�Ľ⼯��x��-1���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com