
【题目】如图,在正方形ABCD的外侧,作等边![]() ADE,则
ADE,则![]() BED的度数是 .
BED的度数是 .

 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案科目:初中数学 来源: 题型:
【题目】用两个全等的直角三角形拼下列图形:①平行四边形;②矩形;③梯形;④正方形;⑤等腰三角形;⑥等边三角形;可以拼成的图形是 ( )
A、①④⑤ B、②⑤⑥ C、①②③ D、①②⑤
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,点C,D分别在两个半圆上(不与点A、B重合),AD、BD的长分别是关于x的方程![]() =0的两个实数根.
=0的两个实数根.
(1)求m的值;
(2)连接CD,试探索:AC、BC、CD三者之间的等量关系,并说明理由;
(3)若CD=![]() ,求AC、BC的长.
,求AC、BC的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB∥CD,∠ABK的角平分线BE的反向延长线和∠DCK的角平分线CF的反向延长线交于点H,∠K﹣∠H=27°,则∠K=( )
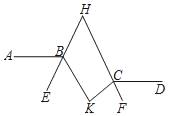
A. 76° B. 78° C. 80° D. 82°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图:在平面直角坐标系中,O为坐标原点,四边形OABC是长方形,点A、C、D的坐标分别为A(9,0)、C(0,4),D(5,0),点P从点O出发,以每秒1个单位长度的速度沿O[Math Processing Error] ![]()
![]() C[Math Processing Error]
C[Math Processing Error] ![]()
![]() B[Math Processing Error]
B[Math Processing Error] ![]()
![]() A运动,点P的运动时间为t秒.
A运动,点P的运动时间为t秒.
(1)当t=5时, P点坐标为____________;
(2)当t>4时,OP+PD有最小值吗?如果有,请算出该最小值,如果没有,请说明理由;
(3)当t为何值时,△ODP是腰长为5的等腰三角形?(直接写出t的值).


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】通过类比联想、引申拓展研究典型题目,可达到解一题知一类的目的.下面是一个案例.
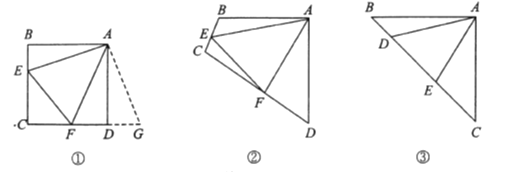
原题:如图①,点![]() 分别在正方形
分别在正方形![]() 的边
的边![]() 上,
上, ![]() ,连接
,连接![]() ,则
,则![]() ,试说明理由.
,试说明理由.
(1)思路梳理
因为![]() ,所以把
,所以把![]() 绕点
绕点![]() 逆时针旋转90°至
逆时针旋转90°至![]() ,可使
,可使![]() 与
与![]() 重合.因为
重合.因为![]() ,所以
,所以![]() ,点
,点![]() 共线.
共线.
根据 ,易证![]() ,得
,得![]() .请证明.
.请证明.
(2)类比引申
如图②,四边形![]() 中,
中, ![]() ,
, ![]() ,点
,点![]() 分别在边
分别在边![]() 上,
上, ![]() .若
.若![]() 都不是直角,则当
都不是直角,则当![]() 与
与![]() 满足等量关系时,
满足等量关系时, ![]() 仍然成立,请证明.
仍然成立,请证明.
(3)联想拓展
如图③,在![]() 中,
中, ![]() ,点
,点![]() 均在边
均在边![]() 上,且
上,且![]() .猜想
.猜想![]() 应满足的等量关系,并写出证明过程.
应满足的等量关系,并写出证明过程.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知直线y=2x-5与x轴和y轴分别交于点A和点B,点C(1,n)在直线AB上,点D在y轴的负半轴上,且CD=![]() .
.
(1)求点C、点D的坐标.
(2)若P为y轴上的点,当△PCD为等腰三角形时,求点P的坐标.
(3)若点M为x轴上一动点(点M不与点O重合),N为直线y=2x-5上一动点,是否存在点M、N,使得△AMN与△AOB全等?若存在,求出点N的坐标;若不存在,请说明理由.


图1 图2
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com