练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图所示，在下面由火柴棒拼出的一系列的图形中，第n个图形由n个正方形组成．

    （1）第2个图形中，火柴棒的根数是________；

    （2）第3个图形中，火柴棒的根数是________；

    （3）第4个图形中，火柴棒的根数是_______；

    （4）第n个图形中，火柴棒的根数是_______ ．

    【答案】（1）7；（2）10；（3）13；（4）3n+1.

    【解析】

    （1）（2）（3）图形中的火柴棒根数可以点数得到．
    （4）根据（1）（2）（3）的结果总结规律，从第一个开始每增加一个正方形火柴棒数增加3个，则第n个图形中应用的火柴棒数为：4+3（n-1）．

    解：根据已知图形可以发现：
    （1）第2个图形中，火柴棒的根数是7；
    （2）第3个图形中，火柴棒的根数是10；
    （3）第4个图形中，火柴棒的根数是13；
    （4）∵每增加一个正方形火柴棒数增加3，
    ∴第n个图形中应有的火柴棒数为：4+3（n-1）=3n+1．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图,已知∠BDG+∠EFG=180°,∠DEF=∠B,试判断∠AED与∠C的大小关系,并加以说明.

    解:∠AED=∠C.

    理由:∵∠EFD+∠EFG=180°( ),

    ∠BDG+∠EFG=180°(已知)

    ∴∠BDG =∠EFD ( ),

    ∴BD∥EF( ),

    ∴∠BDE+∠DEF =180°( ).

    又∵∠DEF=∠B( ),

    ∴∠BDE+∠B =180°( ),

    ∴DE∥BC( ),

    ∴∠AED=∠C( ).

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】（1）2019年4月，中国新闻出版研究院发布了《第十六次全国国民阅读调查报告》，以下是小明根据该报告提供的数据制作的“2017-2018年我国未成年人图书阅读率统计图”的一部分.

    报告中提到，2018年9-13周岁少年儿童图书阅读率比2017年提高了3.1个百分点，2017年我国0-17周岁未成年人图书阅读率为84.8%.

    根据以上信息解决下列问题：

    ①写出图1中a的值；

    ②补全图1；

    （2）读书社的小明在搜集资料的过程中，发现了《人民日报》曾经介绍过多种阅读法，他在班上同学们介绍了其中6种，并调查了全班40名同学对这6种阅读法的认可程度，制作了如下的统计表和统计图：

    根据以上信息解决下列问题：

    ①补全统计表及图2；

    ②根据调查结果估计全年级500名同学最愿意使用“.精华提炼法”的人数.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】若抛物线L：y=ax2+bx+c（a，b，c是常数，abc≠0）与直线l都经过y轴上的一点P，且抛物线L的顶点Q在直线l上，则称此直线l与该抛物线L具有“一带一路”关系．此时，直线l叫做抛物线L的“带线”，抛物线L叫做直线l的“路线”．

    （1）若直线y=mx+1与抛物线y=x2﹣2x+n具有“一带一路”关系，求m，n的值；

    （2）若某“路线”L的顶点在反比例函数y=的图象上，它的“带线”l的解析式为y=2x﹣4，求此“路线”L的解析式；

    （3）当常数k满足≤k≤2时，求抛物线L：y=ax2+（3k2﹣2k+1）x+k的“带线”l与x轴，y轴所围成的三角形面积的取值范围．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

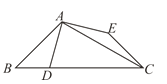
    【题目】如图，△ABC中，∠ABC＝45°，∠BCA＝30°，点D在BC上，点E在△ABC外，且AD＝AE＝CE，AD⊥AE，则的值为____________．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某服装厂承揽一项生产夏凉小衫1600件的任务，计划用t天完成．

    （1）写出每天生产夏凉小衫w（件）与生产时间t（天）（t＞4）之间的函数关系式;

    （2）由于气温提前升高，商家与服装厂商议调整计划，决定提前4天交货，那么服装厂每天要多做多少件夏凉小衫才能完成任务？

    【答案】（1）；（2）

    【解析】试题分析：（1）根据实际意义可列出夏凉小衫w（件）与生产时间t（天）（t＞4）之间的函数关系式；

    （2）根据题意列出t﹣4对应的式子，与（1）中的式子相减即可．

    试题解析：（1）由题意可得，函数关系式为：w=（）；

    （2）==．（或）．

    答：每天多做（或）件夏凉小衫才能完成任务．

    考点：反比例函数的应用．

    【题型】解答题
    【结束】
    13

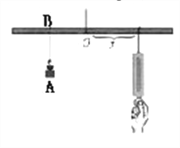
    【题目】如图所示，小华设计了一个探究杠杆平衡条件的实验：在一根匀质的木杆中点O左侧固定位置B处悬挂重物A，在中点O右侧用一个弹簧秤向下拉，改变弹簧秤与点O的距离x（cm），观察弹簧秤的示数y（N）的变化情况。实验数据记录如下：

    x（cm）

    …

    10

    15

    20

    25

    30

    …

    y（N）

    …

    30

    20

    15

    12

    10

    …

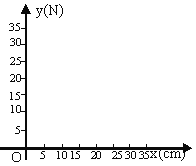
    （1）把上表中x，y的各组对应值作为点的坐标，在坐标系中描出相应的点，用平滑曲线连接这些点并观察所得的图象，猜测y（N）与x（cm）之间的函数关系，并求出函数关系式；

    （2）当弹簧秤的示数为24N时，弹簧秤与O点的距离是多少cm？

    随着弹簧秤与O点的距离不断减小，弹簧秤上的示数将发生怎样的变化？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某校为美化校园，计划对面积为1800m2的区域进行绿化，安排甲、乙两个工程队完成.已知甲队每天能完成绿化的面积是乙队每天能完成绿化的面积的2倍，并且在独立完成面积为400 m2区域的绿化时，甲队比乙队少用4天.

    （1）求甲、乙两工程队每天能完成绿化的面积分别是多少m2？

    （2）若学校每天需付给甲队的绿化费用是0.4万元，乙队为0.25万元，要使这次的绿化总费用不超过8万元，至少应安排甲队工作多少天？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在中，，，，点在上运动，设长为，的面积为.当从小到大变化时，也随之变化.

    (1)求出与之间的关系式.

    (2)完成下面的表格

    4

    5

    6

    7

    6

    (3)由表格看出当每增加时，如何变化？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】问题情境：如图1，AB∥CD，∠PAB=130°，∠PCD=120°，求∠APC的度数．

    小明的思路是：过P作PE∥AB，通过平行线性质来求∠APC．

    (1)按小明的思路，易求得∠APC的度数为_____度；

    (2)问题迁移：如图2，AB∥CD，点P在射线OM上运动，记∠PAB=α，∠PCD=β，当点P在B、D两点之间运动时，问∠APC与α、β之间有何数量关系？请说明理由；

    (3)在(2)的条件下，如果点P在B、D两点外侧运动时（点P与点O、B、D三点不重合），请直接写出∠APC与α、β之间的数量关系．

    查看答案和解析>>

    同步练习册答案