Question

【题目】已知△ABC中,AH⊥BC，垂足为H,若AB+BH=CH,∠ABH=80°,则∠BAC=_________ 。

Answer 1

【答案】60°或40°

【解析】

分锐角三角形和钝角三角形两种情况讨论：锐角三角形时，在CH上截取DH=BH，连接AD，即可得到△ABH≌△ADH，进而得到CD=AD，再由三角形外角的性质即可得出∠B的大小；钝角三角形时，直接由三角形外角的性质即可得出∠B的大小.

当△ABC为锐角三角形时，

在CH上截取DH=BH，连接AD，如图：

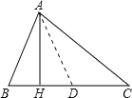
∵AH⊥BC，
∴∠AHB=∠AHD=90°，
在△ABH≌△ADH中，
∵

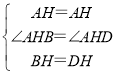
∴△ABH≌△ADH(SAS)，
∴AD=AB，∠ABH=∠ADB=80°，∠BAH=∠DAH，
∵AB+BH= CH，HD+CD=CH
∴AD=CD
∴∠C=∠DAC=40，
∴∠．

当△ABC为钝角三角形时，

如图：

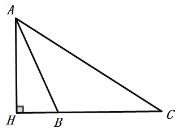
∵AB+BH= CH，BC+ BH =CH
∴AB=CB

∴∠BAC=∠C=40，
故答案为：60°或40°