
【题目】如图,在![]() 中,
中,![]() ,
,![]() 于点
于点![]() ,
,![]() 于点
于点![]() ,
,![]() ,
,![]() ,
,![]() 与
与![]() 交于点
交于点![]() ,连接
,连接![]() ,则
,则![]() 的长为__________.
的长为__________.

【答案】![]()
【解析】
(1)由AD⊥BC于点D,∠BAD=45°,就可以得出AD=BD,再由直角三角形的性质求出∠DAC=∠DBE就可以得出△ADC≌△BDF,则可以得出CD=ED,由勾股定理就可以求出CF,根据等腰三角形的性质就可以求出AE=CE,从而求出结论.
∵AD⊥BC,
∴∠ADB=∠ADC=90°.
∴∠ACD+∠DAC=90°.
∵∠BAD=45°,
∴∠ABD=45°,
∴∠BAD=∠DBA,
∴AD=BD.
∵BE⊥AC,
∴∠BEC=90°,
∴∠ACD+∠EBC=90°,∠ADB=∠ADC
∴∠DAC=∠DBF.
在△ADC和△BDF中,
 ,
,
∴△ADC≌△BDF(ASA);
∴DC=DF.
∵CD=![]() ,
,
∴DF=![]() .
.
在Rt△CDF中,由勾股定理,得
CF=2.
∵AB=BC,BE⊥AC,
∴AE=CE,
∴BE是AC的中垂线,
∴AF=CF,
∴AF=2,
∵AD=AF+DF,
∴AD=2+![]() .
.
故答案为:2+![]() .
.


 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案 名校提分一卷通系列答案
名校提分一卷通系列答案 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案科目:初中数学 来源: 题型:
【题目】锐锐参加我市电视台组织的“牡丹杯”智力竞答节目,答对最后两道单选题就顺利通关,第一道单选题有3个选项,第二道单选题有4个选项,这两道题锐锐都不会,不过锐锐还有两个“求助”可以用(使用“求助”一次可以让主持人去掉其中一题的一个错误选项).
(1)如果锐锐两次“求助”都在第一道题中使用,那么锐锐通关的概率是________;
(2)如果锐锐两次“求助”都在第二道题中使用,那么锐锐通关的概率是________;
(3)如果锐锐每道题各用一次“求助”,请用树状图或者列表来分析他顺利通关的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线![]() 的解析式为
的解析式为![]() ,直线
,直线![]() 的解析式为
的解析式为![]() ,与
,与![]() 轴,
轴,![]() 轴分别交于点
轴分别交于点![]() ,点
,点![]() ,直线
,直线![]() 与
与![]() 交于点
交于点![]() .
.

(1)求点![]() ,点
,点![]() ,点
,点![]() 的坐标,并求出
的坐标,并求出![]() 的面积;
的面积;
(2)若直线 ![]() 上存在点
上存在点![]() (不与
(不与![]() 重合),满足
重合),满足![]() ,请求出点
,请求出点![]() 的坐标;
的坐标;
(3)在![]() 轴右侧有一动直线平行于
轴右侧有一动直线平行于![]() 轴,分别与
轴,分别与![]() ,
,![]() 交于点
交于点![]() ,且点
,且点![]() 在点
在点![]() 的下方,
的下方,![]() 轴上是否存在点
轴上是否存在点![]() ,使
,使![]() 为等腰直角三角形?若存在,请直接写出满足条件的点
为等腰直角三角形?若存在,请直接写出满足条件的点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某水果批发商场销售一种高档水果,如果每千克盈利10元,每天可售出500千克,经市场调查发现,在进货价不变的情况下.若每千克涨价1元,日销售量将减少20千克.
(1)现该商场要保证每天盈利6000元,同时又要使顾客得到实惠,那么每千克应涨价多少元?
(2)每千克水果涨价多少元时,商场每天获得的利润最大?获得的最大利润是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=2x+3与x轴相交于点A,与y轴相交于点B.
(1)求点A,B的坐标;
(2)求当x=-2时,y的值,当y=10时,x的值;
(3)过点B作直线BP与x轴相交于点P,且使OP=2OA,求△ABP的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为倡导低碳生活,绿色出行,某自行车俱乐部利用周末组织“远游骑行”活动,自行车队从甲地出发,目的地为乙地,在自行车队出发![]() 小时后,恰有一辆邮政车从甲地出发,沿自行车队行进路线前往乙地,到达乙地后立即按原路返回甲地.自行车队与邮政车行驶速度均保持不变,并且邮政车行驶速度是自行车队行驶速度的
小时后,恰有一辆邮政车从甲地出发,沿自行车队行进路线前往乙地,到达乙地后立即按原路返回甲地.自行车队与邮政车行驶速度均保持不变,并且邮政车行驶速度是自行车队行驶速度的![]() 倍.如图所示的是自行车队、邮政车离甲地的路程
倍.如图所示的是自行车队、邮政车离甲地的路程![]() 与自行车队离开甲地的时间
与自行车队离开甲地的时间![]() 的关系图象,请根据图象提供的信息,回答下列问题.
的关系图象,请根据图象提供的信息,回答下列问题.

(1)自行车队行驶的速度是 ;邮政车行驶的速度是 ;![]() .
.
(2)邮政车出发多少小时与自行车队相遇?
(3)当邮政车与自行车队相距![]() 时,此时离邮政车出发经过了多少小时?
时,此时离邮政车出发经过了多少小时?
查看答案和解析>>
科目:初中数学 来源: 题型:
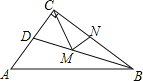
【题目】如图,△ABC中,∠ACB=90°,AC =3,BC =4,AB=5,BD平分∠ABC,如果M、N分别为BD、BC上的动点,那么CM+MN的最小值是____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等边△ABC中,BD=CE,将线段AE沿AC翻折,得到线段AM,连结EM交AC于点N,连结DM、CM以下说法:①AD=AM,②∠MCA=60°,③CM=2CN,④MA=DM中,正确的有( )

A. 1个B. 2个C. 3个D. 4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com