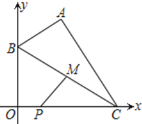
【题目】在平面直角坐标系中，已知
、
，B为y轴上的动点，以AB为边构造
，使点C在x轴上，
为BC的中点，则PM的最小值为______．
【答案】
【解析】
如图，作AH⊥y轴于H，CE⊥AH于E．则四边形CEHO是矩形，OH=CE=4，由△AHB∽△CEA，得
，推出
，推出AE=2BH，设BH=x则AE=2x，推出B（0，4﹣x），C（2+2x，0），由BM=CM，推出M（1+x，
），可得PM
，由此即可解决问题．
如图，作AH⊥y轴于H，CE⊥AH于E．则四边形CEHO是矩形，OH=CE=4．
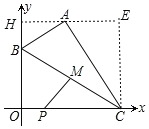
∵∠BAC=∠AHB=∠AEC=90°，∴∠ABH+∠HAB=90°，∠HAB+∠EAC=90°，∴∠ABH=∠EAC，∴△AHB∽△CEA，∴，∴，∴AE=2BH，设BH=x则AE=2x，∴OC=HE=2+2x，OB=4﹣x，∴B（0，4﹣x），C（2+2x，0）．
∵BM=CM，∴M（1+x，）．
∵P（1，0），∴PM，∴x
时，PM有最小值，最小值为．
故答案为：．
科目：初中数学 来源： 题型：
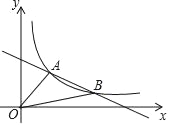
【题目】如图，一次函数y1＝﹣
x+4的图象与反比例函数y2＝
的图象交于A（2，3），B（6，n）两点
（1）观察图象当y1＞y2时，x的取值范围是 ；
（2）求反比例函数的解析式及B点坐标；
（3）求△OAB的面积．
查看答案和解析>>
科目：初中数学 来源： 题型：
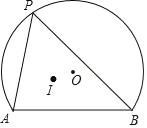
【题目】如图，AB为弓形AB的弦，AB＝2
，弓形所在圆⊙O的半径为2，点P为弧AB上动点，点I为△PAB的内心，当点P从点A向点B运动时，点I移动的路径长为_____．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知如图 1，在△ABC 中，∠ACB＝90°，BC＝AC，点 D 在 AB 上，DE⊥AB交 BC 于 E，点 F 是 AE 的中点
（1） 写出线段 FD 与线段 FC 的关系并证明；
（2） 如图 2，将△BDE 绕点 B 逆时针旋转α（0°＜α＜90°），其它条件不变，线段 FD 与线段 FC 的关系是否变化，写出你的结论并证明；
（3） 将△BDE 绕点 B 逆时针旋转一周，如果 BC＝4，BE＝2
，直接写出线段 BF 的范围．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，旗杆AB的顶端B在夕阳的余辉下落在一个斜坡上的点D处，某校数学课外兴趣小组的同学正在测量旗杆的高度，在旗杆的底部A处测得点D的仰角为15°，AC=10米，又测得∠BDA=45°．已知斜坡CD的坡度为i=1：
，求旗杆AB的高度（≈1.7，结果精确到个位）．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】“绿水青山就是金山银山”，为保护生态环境，A，B两村准备各自清理所属区域养鱼网箱和捕鱼网箱，每村参加清理人数及总开支如下表：
村庄 | 清理养鱼网箱人数/人 | 清理捕鱼网箱人数/人 | 总支出/元 |
A | 15 | 9 | 57000 |
B | 10 | 16 | 68000 |
（1）若两村清理同类渔具的人均支出费用一样，求清理养鱼网箱和捕鱼网箱的人均支出费用各是多少元；
（2）在人均支出费用不变的情况下，为节约开支，两村准备抽调40人共同清理养鱼网箱和捕鱼网箱，要使总支出不超过102000元，且清理养鱼网箱人数小于清理捕鱼网箱人数，则有哪几种分配清理人员方案？
查看答案和解析>>
科目：初中数学 来源： 题型：
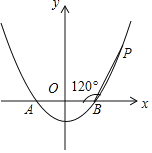
【题目】如图，已知抛物线
与x轴相交于A，B两点，点P是抛物线上一点，且
，
．
求该抛物线的表达式；
设点
为抛物线上的一个动点，当点M在曲线BA之间
含端点
移动时，求
的最大值及取得最大值时点M的坐标．
查看答案和解析>>
科目：初中数学 来源： 题型：
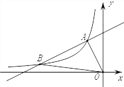
【题目】如图，一次函数y＝k1x＋b的图象与反比例函数y＝
(x＜0)的图象相交于点A(－1，2)、点B(－4，n)．
(1)求此一次函数和反比例函数的表达式；
(2)求△AOB的面积；
(3)在x轴上存在一点P，使△PAB的周长最小，求点P的坐标．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
